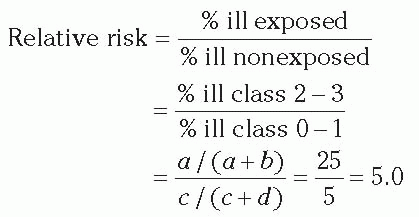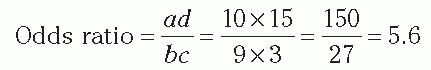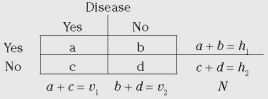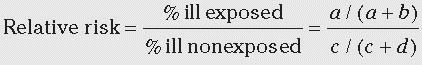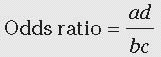Modern Quantitative Epidemiology in the Healthcare Setting
Jerome I. Tokars1
1The findings and conclusions in this report are those of the author and do not necessarily represent the official position of the Centers for Disease Control and Prevention.
I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely, in your thoughts, advanced to the stage of Science, whatever the matter may be.
—Lord Kelvin
The job of the hospital epidemiologist is an intensely political one, into which we can occasionally interject some science.
—Jonathan Freeman
This chapter is about quantitative epidemiology, a term without a formal definition. However, epidemiology can be defined as “the study of the distribution and determinants of health-related states or events in specified populations, and the application of this study to control of health problems” (1). “Distribution” refers to rates of disease overall and in various subgroups; for example, what percent of patients having cardiac surgery develop a surgical site infection? Assembling such rates requires an important series of steps, including determining which diseases are important, how they should be defined, and by what practical means they can be measured. “Study of … determinants of health-related states,” or risk factors for disease, is the part of the definition closest to quantitative epidemiology. For example, what determines whether one patient gets a surgical site infection while another does not, or why the infection rate is higher at one hospital than at another? “Application of this study to control of health problems” is the all-important final step, requiring wisdom, judgment, and political savvy. Given the difficulty of this final step, we should at least be sure that we have done the best possible job at quantitative epidemiology, that is, of analyzing and presenting the data needed for decision making.
In one sense, epidemiology is merely “quantified common sense.” For example, the simple observation that “our infection rate is higher than theirs because our patients are sicker than theirs” describes what epidemiologists call confounding. Confounding bedevils a variety of activities in healthcare epidemiology, including the comparisons of disease rates among hospitals that underlie interhospital comparisons (benchmarking) and quality assurance programs. Simply comparing crude infection or death rates among hospitals, without accounting for factors such as severity of illness, leads to obviously incorrect conclusions. While the concept of confounding may be intuitive, there is considerable complexity in application of the methods of quantitative epidemiology to deal with confounding.
It is difficult to determine the boundary between quantitative epidemiology and a related discipline, statistics. Many healthcare epidemiologists have taken introductory statistics courses, but such entry-level courses are becoming less and less adequate with each passing year. A study of articles in a prominent medical journal showed substantial increases in the use of advanced methods such as multiple regression (from 5% of articles in 1978-1979 to 51% of articles in 2004-2005), survival methods (from 11% to 61%), and power analyses (from 3% to 39%) (2). In 2004 to 2005, 79% of the articles used methods beyond the scope of introductory statistics courses. Greater knowledge of quantitative epidemiology/statistics is needed both to interpret the infection control literature and to practice healthcare epidemiology.
HISTORY OF EPIDEMIOLOGY
A famous early example of applied epidemiology is the work of Dr. John Snow, a physician in London during the cholera epidemic of 1855 (3). At that time, the germ theory of disease had not been accepted and the pathogen causing cholera, Vibrio cholerae, was unknown. Whereas the prevailing view during this period was that disease was caused by a miasm or cloud, Snow inferred from epidemiologic evidence that cholera was a water-borne illness. He constructed a spot map of cholera cases and noted a cluster of cases near a water pump on London’s Broad Street, the so-called Broad Street pump. This early use of a spot map to find the putative cause of an outbreak is an example of descriptive epidemiology. He also
performed several analytic studies, noting that the rate of cholera was higher for people who obtained water from more polluted areas of the Thames. His well-known intervention was to remove the handle from the Broad Street pump, thereby preventing the use of this contaminated water, after which cases of cholera in the vicinity were said to have decreased. This example illustrates that epidemiologists can define the mechanism of disease spread and institute control measures before the agent causing disease is discovered. More recent examples of this power of epidemiology include Legionnaires’ disease and human immunodeficiency virus disease; for both diseases, the mechanism of spread and means of prevention were inferred by epidemiologists before the microbe was discovered in the laboratory.
performed several analytic studies, noting that the rate of cholera was higher for people who obtained water from more polluted areas of the Thames. His well-known intervention was to remove the handle from the Broad Street pump, thereby preventing the use of this contaminated water, after which cases of cholera in the vicinity were said to have decreased. This example illustrates that epidemiologists can define the mechanism of disease spread and institute control measures before the agent causing disease is discovered. More recent examples of this power of epidemiology include Legionnaires’ disease and human immunodeficiency virus disease; for both diseases, the mechanism of spread and means of prevention were inferred by epidemiologists before the microbe was discovered in the laboratory.
DESCRIPTIVE VERSUS ANALYTIC EPIDEMIOLOGY
In descriptive epidemiology, we describe characteristics of the cases and generate hypotheses. The line list of cases, case series, epidemic curves, and spot maps are examples. In analytic epidemiology, we use comparison groups, calculate statistics, and test hypotheses. Many outbreaks and other problems in healthcare epidemiology can be solved by thoughtful examination of descriptive data without the use of analytic epidemiology. However, the increasingly complex nature of healthcare and associated illness demands that we have a firm grounding in analytic or quantitative epidemiology, which is the main focus of this chapter.
MEASURES OF FREQUENCY
Proportions (synonyms are probability, risk, and percentage) are the simplest way to represent how often something occurs. A proportion is the ratio of a part to the whole; that is, the numerator of the ratio is included in the denominator. The proportion with disease is the number of people who get the disease divided by the total number at risk for the disease; that is, proportion ill = number ill/(number ill + number well). The probability of pulling an ace from a deck of cards is 4/52 = 7.7%. Proportions can be represented by a fraction (e.g., 0.077) or a percentage (e.g., 7.7%) and can range from 0 to 1.0 or from 0% to 100%. Proportions cannot be >1.0 or 100% since, using proportions, each entry in the denominator can have at most one entry in the numerator. A proportion is unitless, because the numerator and denominator have the same units. The proportion is the measure of frequency used in cohort studies and to calculate the relative risk.
Odds represent the ratio of a part to the remainder or the probability that an event will occur divided by the probability that it will not occur. Unlike in proportions, the numerator of the ratio is not included in the denominator. The odds of a disease occurring equal the number of people with the disease divided by the number without the disease; that is, odds of illness = number ill/number well. The odds of pulling an ace from a deck of cards are 4/48 = 8.3%. Note that the odds of illness are always higher than a corresponding proportion ill, because the denominator is smaller for odds. Odds are unitless and have bounds of zero to infinity. Odds are used in case-control studies and to calculate the odds ratio.
A rate, in contrast to proportions and odds, has different units of measure in the numerator and denominator, as in 55 miles/hour or 20 healthcare-associated infections/1,000 observed patient-days. A rate can have any value from zero to infinity. Rates are used in incidence density analyses.
Common Usage
The proportion ill, especially in outbreaks, is often called an “attack rate,” although strictly speaking it is a misnomer to refer to a proportion as a rate. This chapter follows common usage in using the following terms interchangeably with proportion ill: percent ill, attack rate, and rate of illness.
Cumulative Incidence Versus Incidence Density
In a cumulative incidence study, time at risk is not taken into account; the denominator is the total number of persons at risk, and the proportion with disease (or proportion with potential risk factors for disease) is calculated. The cohort and case-control studies presented in the following section are examples of cumulative incidence. In an incidence density study, time at risk is accounted for; the denominator is person-time at risk and a rate of illness (e.g., infections per 1,000 patientdays) is calculated. This type of study is considered later in this chapter.
BASIC STUDY DESIGN
There are three types of analytic study: cohort, casecontrol, and cross-sectional. The goal of analytic epidemiologic studies is to discover a statistical association between cases of disease and possible causes of disease, called exposures. A first step in any such study is the careful definition of terms used, especially defining what clinical and laboratory characteristics are required to indicate a case of disease.
The Cohort Study and Relative Risk
Prospective Cohort Study There are several subtypes of cohort study, but all have certain common features and are analyzed the same way. In the prospective cohort study, we identify a group of subjects (e.g., persons or patients) who do not have the disease of interest. Then, we determine which subjects have some potential risk factor (exposure) for disease. We follow the subjects forward in time to see which subjects develop disease. The purpose is to determine whether disease is more common in those with the exposure (“exposed”) than in those without the exposure (“nonexposed”). Those who develop disease are called “cases,” and those who do not develop disease are “noncases” or “controls.”
A classic example of a prospective cohort study is the Framingham study of cardiovascular disease, which began in 1948 (3). Framingham is a city about 20 miles from Boston with a population of about 300,000, which was considered to be representative of the US population. A random sample of 5,127 men and women, age 30 to 60 years and without evidence of cardiovascular disease, was enrolled in 1948. At each subject’s enrollment, researchers recorded gender and the presence or absence of many exposures, including smoking, obesity, high blood pressure, high cholesterol, low level of physical activity, and family history of cardiovascular disease. This cohort was then followed forward in time by examining the subjects every 2 years and daily checking of the only local hospital for admissions for cardiovascular disease.
Note several features of this study. The study was truly prospective in that it was started before the subjects developed disease. Subjects were followed over many years and monitored to determine if disease occurred, that is, if they became “cases.” This is an incidence study, in which only new cases of disease were counted (because persons with cardiovascular disease in 1948 were not eligible for enrollment). In an incidence study, it is necessary to specify the study period, that is, how long the subjects were allowed to be at risk before we looked to see whether they had developed disease.
The Framingham study allowed investigators to determine risk factors for a number of cardiovascular disease outcomes, such as anginal chest pain, myocardial infarction (heart attack), death due to myocardial infarction, and stroke. One finding of this study was that smokers had a higher rate of myocardial infarction than nonsmokers. An advantage of this study design is that it is very flexible, in that the effect of many different exposures on many different outcome variables can be determined. The disadvantages are the time, effort, and cost required.
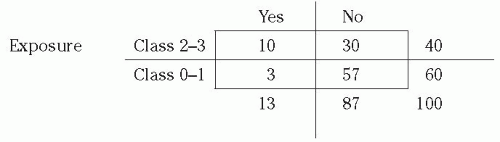
Relative Risk Performing hospital surveillance for surgical site infections (SSIs) is an example of a prospective cohort study. Assume that during one year at hospital X, 100 patients had a certain operative procedure. Of these, 40 were wound class 2 to 3 and 60 were class 0 to 1. Note that wound class was determined before it was known which patients were going to develop SSI; this makes it a prospective cohort study. A subgroup or sample of patients was not selected; that is, the entire group was studied. When the patients were followed forward in time, the following was found: of 40 patients with class 2 to 3 procedures, 10 developed SSI; of 60 patients with class 0 to 1 procedures, 3 developed SSI.
Cohort study data are commonly presented in a 2 × 2 table format. The general form of the 2 × 2 table is shown in Table 2-1, and the 2 × 2 table for this SSI example is shown below. Notice that the columns denote whether disease (SSI) was present and the rows whether exposure (wound class 2-3) was present. In this example, exposed means being class 2 to 3 and nonexposed means being class 0 to 1. In the 2 × 2 table below, the total number of cases is 13, total noncases is 87, total exposed is 40, total nonexposed is 60, and total patients is 100.
TABLE 2-1 The 2 × 2 Table and Associated Formulas | |||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
 Disease: Surgical Site Infection |
In the exposed group, the proportion ill = 10/40 = 0.25 or 25%. In the nonexposed group, the proportion ill = 3/60 = 0.05 or 5%. We compare the frequency of disease in the exposed versus nonexposed groups by calculating the relative risk (often called risk ratio). The relative risk of 5.0 means that patients in wound class 2 to 3 were five times more likely to develop SSI than were patients in wound class 0 to 1.
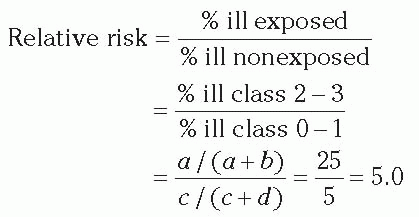
Retrospective Cohort Study A retrospective cohort study is started after disease has developed. A study period
(start date and stop date) is decided upon. Using patient records, we look back in time to identify a group (cohort) of subjects that did not have the disease at the start time. We then use patient records to determine whether each cohort member had a certain exposure. Again using patient records, we determine which cohort members developed disease during the study period. Finally, we calculate the percent with disease in those with the exposure and those without the exposure and compare the two.
(start date and stop date) is decided upon. Using patient records, we look back in time to identify a group (cohort) of subjects that did not have the disease at the start time. We then use patient records to determine whether each cohort member had a certain exposure. Again using patient records, we determine which cohort members developed disease during the study period. Finally, we calculate the percent with disease in those with the exposure and those without the exposure and compare the two.
The following is an example of a retrospective cohort study based on the SSI example above. Hospital X noted that the overall SSI rate of 13% was higher than in previous years. We want to determine whether a new surgeon (surgeon A) was responsible for the increase. The prospective surveillance system did not routinely record the surgeon performing each procedure, so we pull the records from each procedure and record whether or not surgeon A was involved. We find that surgeon A operated on 20 patients,3 of whom later developed SSI. Among the 80 other patients, 10 developed SSI. The percent ill in the exposed group (surgeon A) = 3/20 = 15%. The percent ill for other surgeons (nonexposed) = 10/80 = 12.5%. The relative risk = 15%/12.5% = 1.2.
The interpretation is that patients operated on by surgeon A were 1.2 times (or 20%) more likely to develop disease than patients operated on by other surgeons. Factors to consider in deciding whether surgeon A is truly a cause of the problem are presented below (see Interpretation of Data, Including Statistical Significance and Causal Inference).
To review, this was a retrospective cohort study, since data on the exposure were collected from patient records after we knew which patients had developed SSI. The retrospective nature of data collection is sometimes irrelevant and sometimes a problem. For certain types of data, such as length of hospital stay or death, retrospective data collection will be as good as prospective. However, determining other factors, such as which ancillary personnel treated a given patient, may be difficult to do after the fact, and retrospective studies using such data may be less valid.
Observational Versus Experimental Studies Epidemiologic studies are generally observational; that is, the investigator collects data but does not intervene in patient care. Patients, physicians, nurses, and random processes all play a part in determining exposures in the hospital. The goal of observational studies is to simulate the results of an experimental study (see Quasi-Experimental Studies)
In an experimental study, a group (cohort) of subjects is identified and the investigator assigns some of them to receive treatment A (exposed) and the remainder to receive an alternate treatment B (nonexposed). The patients are followed forward in time, the cases of disease are recorded, and the rates of illness and relative risk are calculated as usual. The experimental study is a special type of a prospective cohort study where the two exposure groups are assigned by the investigator.
Cohort Studies With Subjects Selected Based on Exposure In this type of cohort study, subjects are selected based on exposure. We select two subgroups: one that is exposed and one that is nonexposed. Both groups are followed forward in time to see how many develop disease. Consider the SSI example and surgeon A above. We study all 20 patients operated on by surgeon A (exposed); of the 80 patients operated on by other surgeons, we randomly select 40 (nonexposed). Thus, only 60 patients of the original group of 100 are included in this study.
Note that this is a type of cohort study, not a case-control study. In a case-control study, the subjects are chosen based on whether or not they have disease. In this study, subjects were chosen based on whether or not they had exposure.
The disadvantage of this type of cohort study, where the subjects are selected based on exposure, is that only one exposure (i.e., the exposure that you selected subjects on) can be studied. However, this type of study is very useful for studying an uncommon exposure. In the SSI surveillance example used above, consider the situation if there had been 500 surgical procedures, and surgeon A had performed only 20 of them. If you performed a cohort study of the entire group, you would have to review 500 charts, which would waste time and effort. Instead, you could perform a cohort study of the 20 procedures performed by surgeon A (exposed), and 40 randomly selected procedures performed by other surgeons (nonexposed). The second alternative would be much more efficient.
Cohort Studies—Summary Cohort studies can be prospective or retrospective, observational or experimental. They usually include a whole group of subjects, but studying two subgroups selected based on exposure is also possible. The 2 × 2 table layout and calculations are the same for all types of cohort studies. All have in common that subjects are chosen without regard to whether they develop disease.
The Case-Control Study and Odds Ratio
In a case-control study, we choose subjects for study based on whether they have disease. Since we have to know which subjects developed disease before we select them, case-control studies are always retrospective. We usually study those with disease (cases) and choose a sample of those without disease (controls). We usually study one to four controls per case. The more controls, the greater the chance of finding statistically significant results. However, there is little additional benefit from studying more than four controls per case. Controls are usually randomly selected from subjects present during the study period who did not have disease.
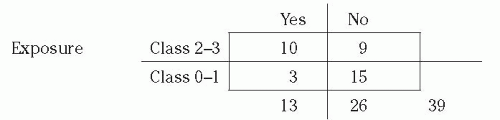
Example: Case-Control Study of Surgical Site Infections This is the same example presented in the section on cohort study and relative risk. At hospital X, 100 patients had a certain operative procedure, 40 class 2 to 3 (exposed) and 60 class 0 to 1 (nonexposed), and 13 developed SSI. To perform a case-control study, we select the 13 patients with SSI (cases) and also study 26 patients who had surgical procedures but did not have SSI (controls). We studied two controls per case, but could have studied fewer or more controls. The controls were randomly chosen from all patients who had the surgical procedure under study but did not develop SSI. From their
medical records, we find which of the subjects had class 2 to 3 procedures and which had class 0 to 1 procedures. Our data showed that, of 13 cases, 10 had class 2 to 3 procedures. Of 26 noncases, 9 had class 2 to 3 procedures. The 2 × 2 table for this example is as follows:
medical records, we find which of the subjects had class 2 to 3 procedures and which had class 0 to 1 procedures. Our data showed that, of 13 cases, 10 had class 2 to 3 procedures. Of 26 noncases, 9 had class 2 to 3 procedures. The 2 × 2 table for this example is as follows:
 Disease: Surgical Site Infection |
In a case-control study, we cannot determine the percent ill in the exposed or nonexposed groups, or the relative risk. In this example, note that the percent ill among class 2 to 3 is NOT = 10/(10 + 9) = 52.6%. However, we can validly calculate the percent of cases that were exposed, 10/13 = 76.9%, and the percent of noncases that were exposed, 9/26 = 34.6%. Note that the cases were much more likely to have the exposure than were the controls. Most importantly, we can calculate the odds ratio (also called the relative odds; Table 2-1) as follows:
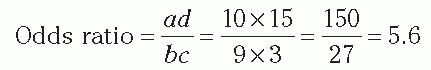
We can interpret the odds ratio as an estimate of the relative risk. Using the case-control method, we estimated that patients in class 2 to 3 were 5.6 times more likely to develop SSI than were patients in class 0 to 1. Note that the odds ratio is similar to, but slightly higher than, the relative risk (5.0) we calculated previously. If the frequency of disease is not too high, that is, is less than approximately 10%, the odds ratio is a good approximation of the relative risk.
The meanings of the letters (i.e., a, b, c, and d) used to represent the 2 × 2 table cells are different in cohort versus case-control studies (Table 2-1). For example, in a cohort study, a denotes the number of cases of disease among exposed persons; in a case-control study, a denotes the number exposed among a group of cases. Although this distinction may not be clear to the novice, it will suffice to keep in mind that in a case-control study, it is not valid to calculate percent ill or relative risk, but it is valid to calculate an odds ratio.
A more in-depth explanation of the odds ratio is as follows. In a case-control study, we actually measure the odds of exposure among those with disease and the odds of exposure among those without disease. The ratio of these two odds is the exposure odds ratio; if equal to 2.0, this would be interpreted as “the odds of exposure are twice as high in those with disease versus those without disease.” However, the exposure odds ratio is not a very useful quantity. Fortunately, it can be proven mathematically that the exposure odds ratio equals the disease odds ratio. Therefore, using our example of 2.0, we can say that the odds of disease are twice as high in those exposed versus those not exposed, which is closer to being useful. Finally, we use the odds ratio as an approximation of the relative risk (where the frequency of disease is not too high) and say simply that those with exposure are twice as likely to get disease.
Selection of Controls Selection of controls is the critical design issue for a case-control study. Controls should represent the source population from which the cases came; represent persons who, if they had developed disease, would have been a case in the study; and be selected independently of exposure (4). It is always appropriate to seek advice when selecting controls, and may be worthwhile to select two control groups to compare the results obtained with each.
An example of incorrect selection of controls is provided by a case-control study of coffee and pancreatic cancer (3,5). The cases were patients with pancreatic cancer, and controls were selected from other inpatients admitted by the cases’ physicians but without pancreatic cancer. The finding was that cases were more likely to have had the exposure (coffee drinking) than the controls, which translated into a significant association between coffee drinking and pancreatic cancer. The problem was that the controls were not selected from the source population of the cases (cases did not arise from hospital inpatients) and thus were not representative of noncases. The physicians admitting patients with cancer of the pancreas were likely to admit other patients with gastrointestinal illness; these control patients were less likely to be coffee drinkers than the general population, possibly because they had diseases that prompted them to avoid coffee. A better control group might have been healthy persons of similar age group to the cases.
More contemporary examples of problematic control selection are studies of the association between vancomycin receipt and vancomycin resistance (6). Cases are often hospitalized patients who are culture positive for vancomycin-resistant enterococci. Controls have often been selected from patients who were culture positive for vancomycin-sensitive enterococci. Using this control group, case-patients will be more likely to have received vancomycin than the controls, resulting in a significant association and elevated odds ratio. The problem is that controls were not representative of the source population and were less likely to have received vancomycin than other patients, since vancomycin would have suppressed or eliminated vancomycin-sensitive microorganisms. Better control groups would be hospital patients similar in age and severity of illness to the cases.
A potential problem is that hospital patients without a positive culture may include some patients who had the microorganism but were not cultured. Inclusion of these patients as controls would bias the odds ratio to 1.0 (null result). An alternative method is to limit controls to those with at least one clinical culture performed. However, this may not be preferable since it results in selection of sicker controls (“severity of illness bias”) and also biases the odds ratio toward 1.0 (7). Another way to look at this issue of potential “contamination” of the control group with unrecognized cases is as follows: in a study design called the case-cohort study, cases are compared with subjects chosen from all patients (i.e., from both cases and noncases); then, the ad/bc statistic equals the relative risk rather than the odds ratio; therefore, inadvertent inclusion of noncases in the control group when performing a casecontrol study may “bias” the odds ratio toward the relative risk and thus be advantageous.
Comparison of Cohort Versus Case-Control Studies
Cohort studies may be prospective or retrospective, but case-control studies are always retrospective. A major advantage of cohort studies is that we can calculate the percent ill and the relative risk. Cohort studies are less subject to bias than case-control studies. The potential disadvantages of cohort studies are that they are more time-consuming and expensive and may require study of a large group to collect information on a small number of cases.
Prospective cohort studies are the premier type of observational study. They provide the strongest evidence; are less subject to bias in collecting exposure data, since exposure is recorded before the subjects develop disease; and are flexible in that it is possible to study many exposures and diseases. The disadvantage is that it may be necessary to follow subjects over a long period of time to determine whether they develop disease.
The advantages of the case-control study are that we can determine risk factors while studying a relatively small group of patients; we can study as many risk factors as desired; and case-control studies are usually quicker, easier, and cheaper than cohort studies. The disadvantages are that the percent ill and relative risk are not determined; only one disease can be studied at a time; and the selection of controls can be subtle and introduces the chance of error. Deciding which is the most appropriate control group for a particular study is a matter of opinion about which even well-trained epidemiologists may disagree.
Cross-Sectional or Prevalence Study
A third type of study (besides cohort and case-control) includes only subjects who are present in a locality at one point in time. Exposure and disease are ascertained at the same time. Depending on the way the subjects were selected, a cross-sectional study may be analyzed as a cohort study or a case-control study.
A cross-sectional study is clearly not an incidence study, which would include as cases only those free of disease at the start of the study and who develop disease during the study period. However, if an entire group present at one point in time is studied, the results can be analyzed in a 2 × 2 table similar to that used for cohort studies. The formula used to calculate a relative risk in a cohort study would yield a prevalence ratio in a cross-sectional study. If the group present at one point in time is sampled as in a case-control study (i.e., the cases and a random selection of noncases are studied), then the odds ratio formula could be used to calculate a prevalence odds ratio.
Incidence Versus Prevalence
Incidence includes only new cases of disease with onset during a study period; the denominator is the number of subjects without disease at the beginning of the study period. Incidence measures the rate at which people without the disease develop the disease during a specified period of time; it is used to study disease etiology (risk).
Prevalence includes both new and old cases that are present at one time and place, measuring the proportion of people who are ill. The commonest measure of prevalence is point prevalence, which is the proportion of individuals who are ill at one point in time. Point prevalence is a unitless proportion. A different measure of prevalence, period prevalence, is the proportion of persons present during a time period with disease. Period prevalence has been criticized as an undefined mixture of both prevalent and incident cases without quantitative use, but is occasionally seen.
Prevalence studies are the ideal way to measure disease burden and plan for needed resources. For example, if we wanted to know how many isolation rooms would be needed for patients with resistant microorganisms, we would want to know average prevalence, that is, the total number of patients with recognized drug-resistant microorganisms of either new or old onset in the hospital at any given time.
Prevalence can also be used as a simple, quick, and dirty way to measure disease frequency and risk factors, but such estimates may be biased by length of stay. It is often said that prevalence equals incidence times duration. That is, prevalence is higher if either incidence is higher or if the duration of the illness is longer. In hospital studies, prevalence is greatly influenced by length of stay and mortality. For example, assuming that ascertainment of vancomycin-resistant enterococci is stable, the prevalence of vancomycin-resistant enterococci in a hospital may decrease because of an effective prevention program, or because patients with this microorganism are being discharged sooner or dying more commonly than had been the case previously.
Point prevalence and incidence density are mathematically linked; in a steady-state or dynamic population, one can be derived from the other. Prevalence can be derived from incidence density and distributions of durations of disease, and incidence density may be derived from prevalence and distributions of durations to date of disease (8, 9, 10, 11).
INTERPRETATION OF DATA, INCLUDING STATISTICAL SIGNIFICANCE AND CAUSAL INFERENCE
Measures of Size of Effect and their Interpretation
The relative risk and the odds ratio measure the size of effect, that is, the magnitude of the association between an exposure and a disease. A relative risk of 1.3 shows a modest association, whereas a value of 20 shows a large association. In general, odds ratios are interpreted in the same manner as relative risks.
Because the relative risk = percent ill exposed/percent ill nonexposed, the relative risk can fall into three categories. First, if the two percents are approximately equal, the relative risk is approximately 1.0; this is a null result showing no association between exposure and disease. Second, if the percent ill is higher in the exposed group, the relative risk is >1.0; exposure is apparently associated with disease, is a risk factor for disease, and may be a cause of disease. Third, if the percent ill is higher in those without exposure,
the relative risk is <1.0; exposure is again apparently associated with disease, but in this instance the exposure prevents disease. An example of a preventive exposure is vaccine use; persons who are “exposed” to the vaccine have a lower rate of disease than those not exposed, leading to a relative risk <1.0. Interpretation of odds ratios as equal to, greater than, or less than 1.0 is similar. To intelligently interpret relative risks and odds ratios, we must in addition understand statistical significance and the distinction between association and causation (presented below).
the relative risk is <1.0; exposure is again apparently associated with disease, but in this instance the exposure prevents disease. An example of a preventive exposure is vaccine use; persons who are “exposed” to the vaccine have a lower rate of disease than those not exposed, leading to a relative risk <1.0. Interpretation of odds ratios as equal to, greater than, or less than 1.0 is similar. To intelligently interpret relative risks and odds ratios, we must in addition understand statistical significance and the distinction between association and causation (presented below).
Relative risks can be interpreted as a percent increase or decrease. For example, a relative risk of 1.5 could be interpreted in two ways: disease is 1.5 times more likely in exposed than in nonexposed, or disease is 50% more likely in exposed than in nonexposed. Similarly, a protective relative risk of 0.6 could be interpreted in two ways: illness was 0.6 times as likely in exposed than in nonexposed, or illness was 40% less likely in the exposed group.
Statistical Significance and p Values
For a given group and time period, an association between exposure and disease might occur due to chance alone. For example, suppose that over many years the rate of SSI at hospital A is the same as that of other hospitals. However, during a given quarter, the rate at hospital A may be higher or lower than average by chance alone. To tell us the probability that the SSI rate at hospital A differed from the rate at other hospitals due to chance alone, we commonly use two measures of statistical significance, the p value and the confidence interval.
The p value measures the probability that a given result, or one more extreme, could have happened by chance alone if there was no association between exposure and diseases. Because computer packages calculate p values automatically, it is more important to know how to interpret than to calculate them. P values range from >0 to 1.0. By convention, a p value ≤.05 indicates statistical significance. This means that there is a ≤5% or ≤1/20 chance that the result we found (or one more extreme) could have occurred by chance alone; exposure is associated with disease. Another way of stating this is that we are 95% certain that this observed difference did not arise by chance alone. If the p value is >.05, the result is not considered statistically significant and could well have happened by chance alone; we do not have evidence that exposure is associated with disease.
The .05 cutoff was not chosen for any particular reason but now is very commonly used. There is not a meaningful difference between p values of .04 and .06; although the latter would not usually be considered statistically significant, in fact there is only a 6% chance that such a result could have occurred by chance alone. The adoption of the arbitrary .05 standard has its unfortunate aspects and is subject to interpretation after considering all of the sources of bias described below. Some published manuscripts describe interesting or important studies where the p value did not reach .05, thus allowing readers to make their own determinations of biologic importance.
Small epidemics, or epidemics that are stopped before there are sufficient cases to demonstrate statistical significance at the .05 level, may be biologically very important, so epidemiologists who work with observational data in hospitals should not consider statistical p values to be of primary interest. Biologic importance and size of effect are much more compelling than p values in the face of an ongoing problem in a hospital.
In biostatistical terms, significance testing can be viewed as follows. We assume the null hypothesis that there is no true difference in rate of illness between the exposed and nonexposed groups. We then compute the p value, that is, probability of the results (or results more extreme) under the null hypothesis. If the p value is low, then apparently the null hypothesis was wrong, and we reject the null hypothesis and embrace the alternative hypothesis, namely, that there is a true difference between exposed and nonexposed (see Chapter 3).
Type I Versus Type II Error The p value required for statistical significance is commonly called the chance of type I error. This means that if we conclude that hospital A has a high (or low) rate of illness based on a p value of .05, there is a 5% chance that we are drawing this conclusion in error. The type I error then indicates the chance of concluding that a difference in rates exists when in fact there is no true difference. Type II error measures the opposite problem—that there really is a difference between the two rates but we erroneously conclude that they are the same. The power of a study (discussed below) = 1—the probability of type II error.
Methods of Calculating p Values P values for 2 × 2 tables may be calculated by the chi-square or Fisher exact methods. The chi-square p value is valid when an expected value (Table 2-1) is not <5; if an expected value is <5, the Fisher exact results should be used. Computer packages commonly calculate expected values and print out a suggestion to use the Fisher exact p value if appropriate. In addition to a simple or uncorrected chi-square value, computer packages may compute a continuity corrected (or Yates corrected) value. The formula for continuity correction involves subtracting 0.5 from each cell in the 2 × 2 table. There are usually not great differences among these chi-square values, and many authorities suggest using the simple or uncorrected value.
The calculation of chi-square value does not differ depending on whether data are from a cohort, case-control, or cross-sectional study. However, the computation of chi-square value is different for incidence density data. Calculation of chi-square value is shown in Table 2-1 and Question 3 in Appendix 1 at the end of this chapter. Later in this chapter we suggest some shareware programs that perform these calculations. When one has the value for chi-square, one can determine the p value by looking it up in a table or by using a statistical program. In Excel, the CHIDIST function calculates the p value for a given chisquare value and number of degrees of freedom.
P values may be one-tailed or two-tailed. Two-tailed p values are usually twice as great as one-tailed values. A two-tailed p value assumes that the rate in the exposed group could have been either higher or lower than in the unexposed group due to chance alone. A one-tailed value recognizes only one of these two possibilities. For example, suppose that a study showed rates of illness significantly lower among those exposed to a putative toxin
than among those not exposed; if the intent had been to conclude that the “toxin” might actually be protective, we should use a two-tailed test; however, if the intent had been to consider such a finding to be spurious and probably due to chance alone and conclude that the toxin has no effect, then we should use a one-tailed test. Although there is no uniform agreement as to whether one- or twotailed results should be used, the majority of authors use two-tailed p values. This suggests that, for uniformity and ease of comparison among studies, two-tailed p values should be the standard.
than among those not exposed; if the intent had been to conclude that the “toxin” might actually be protective, we should use a two-tailed test; however, if the intent had been to consider such a finding to be spurious and probably due to chance alone and conclude that the toxin has no effect, then we should use a one-tailed test. Although there is no uniform agreement as to whether one- or twotailed results should be used, the majority of authors use two-tailed p values. This suggests that, for uniformity and ease of comparison among studies, two-tailed p values should be the standard.
One-tailed tests are standard for noninferiority studies, which are becoming more common in the literature. An example is a trial of whether hepatitis A vaccine is inferior to the standard method, immune globulin, for postexposure prophylaxis (12). Hepatitis rates were 4.4% among those vaccinated and 3.3% among those receiving immune globulin (relative risk = 1.35, two-tailed confidence interval = 0.7-2.67, one-tailed upper confidence limit = 2.40). Since the one-tailed upper confidence limit did not overlap a predetermined relative risk of 3.0, the authors concluded that the vaccine was noninferior. If the rate of hepatitis A had been lower among those receiving vaccine than immune globulin, the authors would have dismissed the finding and not concluded that the vaccine was better. Given this intent, a one-tailed test was appropriate for this study, as it is for other noninferiority trials.
Confidence Intervals
The second way to judge statistical significance is the confidence interval for a relative risk or odds ratio. The confidence interval combines the concepts of size of effect (relative risk) and strength of association (p value). A 95% confidence interval means that, roughly speaking, we are 95% sure that the true relative risk lies between the upper and lower confidence interval limits. For example, assume that a study showed a relative risk of 5.0 with a 95% confidence interval of 1.47 to 17.05. Our best guess is that the relative risk is 5.0, which seems quite high, but we are 95% sure that it lies between 1.47 and 17.05. This is much more informative than simply reporting the probability of our results under the null hypothesis (p value). An additional benefit of the confidence interval is humility; a wide interval points out the uncertainty in our results.
If a 95% confidence interval does not cross 1.0, the result is statistically significant at the .05 level. Remembering the formula for the relative risk, a relative risk >1.0 with a 95% confidence interval excluding 1.0 means that we are 95% sure that the rate of illness in the exposed group is greater than the rate of illness in the nonexposed group.
Causal Inference: Association Versus Causation
A statistical association between an exposure and a disease does not necessarily mean that the exposure caused the disease. Sir Bradford Hill first described a set of logical criteria by which associations could be judged for potential causality. Fulfillment of Hill’s criteria does not guarantee that an association is causal, but failure to meet these criteria generally excludes the possibility of causality. These criteria have changed somewhat over time, but here is a version appropriate for healthcare epidemiology:
Size of effect can be estimated by the relative risk. Large effects are more likely to be causal than small effects. The magnitude of a credible relative risk must depend on the magnitude of the potential sources of bias. Generally, a relative risk >2.0 or <0.5 in a well-done study is difficult to ignore.
Strength of association can be measured by the p value. A relatively weak association can more easily be the result of random or systematic error. A p value near .05 would be considered a weak association. The same information is better presented by the statement that a relative risk 95% confidence bound near 1.0 would be evidence of a weak association.
Consistency: A particular effect should be reproducible in different populations and settings.
Temporality: The cause must precede the effect.
Biologic gradient: There should be a dose-response effect. More exposure should lead to more outcome.
Plausibility of the biologic model: There should be a reasonable biologic model to explain the apparent association. This includes Hill’s criteria of coherence, experimental evidence, and analogy.
ERRORS IN EPIDEMIOLOGIC STUDIES
Epidemiologic studies, even observational studies, involve people and are usually expensive. Therefore, the practical goal is to design a study that requires the least resources yet will provide a good-enough answer to a question. Since the perfect epidemiologic study will never be done, every epidemiologist has to be an expert on sources of error in measurement. For every question or every study, one must review the potential sources of error, estimate their likely direction and magnitude, and then decide what overall effect these distortions might have on the result of the study.
It is worthwhile to distinguish random variation, random error, and systematic error. Random variation is the statistical phenomenon of variability due to chance alone, and is sometimes called background or noise. If we were measuring SSIs, the true underlying SSI rate would vary each month according to many factors, including the mix of surgeons and patients involved; assuming hypothetically that these factors could be held stable, the SSI rate would still vary each month because of chance alone (i.e., random variation). On the other hand, random and systematic errors are produced by inaccuracies in finding or recording data. Random error would occur if we incorrectly measure the SSI rate to be higher than it actually is during some months and lower than it actually is in other months; over many months, these random errors in measurement balance each other and the average value would be correct. Systematic error would occur if we consistently measured the SSI rate as higher or lower than the true rate, and an average over many months would be wrong; systematic error is also called bias. We define validity as getting the right answer, or alternately as a lack of bias.
A related concept is precision, which may be functionally defined as the width of the confidence interval. A narrow
confidence interval indicates high precision; that is, we are confident that the true value is within a narrow range. A confidence interval is narrower when both random variation and random error are low and vice versa. A larger sample size leads to a narrower confidence interval and greater precision. Precision may also be improved by modifying the study design to increase the statistical efficiency by which information is obtained from a given number of study subjects.
confidence interval indicates high precision; that is, we are confident that the true value is within a narrow range. A confidence interval is narrower when both random variation and random error are low and vice versa. A larger sample size leads to a narrower confidence interval and greater precision. Precision may also be improved by modifying the study design to increase the statistical efficiency by which information is obtained from a given number of study subjects.
Selection Bias or Berkson’s Bias
Selection bias occurs when inappropriate subjects are chosen for a study. An example is a study of mortality rates in patients with versus without bacteremia. The problem is that blood cultures are selectively obtained from patients who appear septic, and thus mildly ill patients who may have unrecognized bacteremia are not included as cases. Therefore, cases are not representative of all patients with bacteremia. Including only the sicker cases leads to an overestimate of the mortality associated with bacteremia. Other examples of selection bias are given in the section on selection of controls for case-control study. Selection bias cannot be corrected by data analysis techniques. In traditional surveillance, however, where no selection of subjects occurs, selection bias is not usually a problem.
Misclassification or Information Bias
After subjects are chosen, errors in classification of exposure or outcome are called misclassification. For example, suppose that one is comparing postsurgical infections between thoracic and general surgeons. In this hypothetical hospital, the thoracic surgeons do routine urine cultures for all patients with urinary catheters, sputum cultures for all intubated patients, and vascular catheter tip cultures when catheters are removed. However, the general surgeons obtain cultures only when they feel it is necessary. A comparison of infection rates shows higher infection rates for the thoracic surgeons when all that has really happened is that infection status has been misclassified.
Misclassification may be differential or nondifferential. Differential misclassification means that, in a case-control study, exposure is incorrectly determined to a differing extent among those with versus without disease or, in a cohort study, that disease is incorrectly determined to a differing extent among those with versus without exposure. Differential misclassification may bias the calculated relative risk away from the null value of 1.0, making the relative risk either falsely high (for risk factors with relative risk >1.0) or falsely low (for protective factors with relative risk <1.0). Conversely, nondifferential misclassification would mean that exposure was recorded incorrectly to a similar extent for those with and without disease, or disease was recorded incorrectly to a similar extent in those with and without exposure. This type of misclassification biases the relative risk toward the null value of 1.0.
Note that mere low sensitivity does not mean that data are not useful. The reliability of data primarily depends on how consistent the sensitivity remains in the data collection. National data on sexually transmitted diseases and food-borne illnesses such as salmonella gastroenteritis have a consistent sensitivity of around 0.01 or 1%, but these data remain useful because the sensitivity has been relatively constant at that level over time, so that secular increases or decreases are evident. Data with higher levels of sensitivity but greater variability are actually less reliable in making valid comparisons. Benchmarking comparisons among facilities should be attempted only when a practitioner has some measure of the comparative sensitivities of data from different populations.
A Broader View of Bias
Bias can be more generally defined as a systematic deviation from the truth: any trend in the collection, analysis, interpretation, publication, or review of data that can lead to conclusions that are systematically different from the truth (13). In the analysis phase of a study, if one has a strong preconceived idea of what the answer should be, then a biased analysis and interpretation of the data may result. If one keeps analyzing and reanalyzing data with a view to finding something statistically significant to publish, eventually a satisfactory result will be found. This has been expressed as “If you torture data enough, it will confess to anything.” Publication bias results when studies that show a statistically significant difference between study groups are published, whereas other studies of the same topic that did not show such a difference remain unpublished.
Inaccuracy of Hospital Surveillance
Errors in routine hospital surveillance for healthcareassociated infections could result in either reporting of spurious episodes of infection or lack of reporting of true infections. In practice, the latter problem is much more common. Patients with true healthcare-associated infections escape detection because (a) not all relevant data are present in the medical record or laboratory reports; (b) the data collector may overlook relevant data; and (c) the physician did not order appropriate tests to detect the infection. Estimates of the loss of sensitivity due to (a) and (b) above are shown in Table 2-2. In this table, all sensitivities are related to a composite standard, including data from multiple independent surveys of the medical record, bedside examination, and microbiology laboratory records.
The effect of point (c) above was measured in the Study of the Efficacy of Nosocomial Infection Control (SENIC) (14,15). The overall culturing rate, which was the proportion of patients with signs or symptoms of any infection that had at least one appropriate culture done, was 32% in 1970 and 40% in 1975 to 1976 (14). The proportion of febrile patients from whom at least one appropriate culture was obtained was 28% in 1970 and 45% in 1975 (14). These measures varied substantially from 5% to 95% by hospital type and region of the country. Patients in academic hospitals in the northeast United States had the highest likelihood of being appropriately cultured. It follows that patients in such hospitals were more likely to have a healthcare-associated infection documented. For urinary tract infections, pneumonias, and bacteremias, the lack of availability of objective data was a major determinant of observed rates of infection (15).
The National Nosocomial Infections Surveillance (NNIS) system, now replaced by the National Healthcare Safety Network (NHSN), conducted a study of the accuracy of reporting healthcare-associated infection rates in intensive care unit patients (16). The sensitivity in this study was greatly improved over that found in the SENIC
project, as the NNIS hospitals correctly reported the majority of infections that occurred. Still of concern, however, was the continuing wide range in the sensitivity that varied from 30% to 85%, depending on the site of infection. In this study, substantial numbers of healthcare-associated infections were missed by prospective monitoring and a different large group was missed by retrospective chart review.
project, as the NNIS hospitals correctly reported the majority of infections that occurred. Still of concern, however, was the continuing wide range in the sensitivity that varied from 30% to 85%, depending on the site of infection. In this study, substantial numbers of healthcare-associated infections were missed by prospective monitoring and a different large group was missed by retrospective chart review.
TABLE 2-2 Sensitivities of Methods of Case-Finding for Healthcare-Associated Infections Quantifying Only Omissions from Limited Data Sources and Errors by Surveyors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The implications of these findings for benchmarking rates among hospitals are obvious. There is a disincentive for physicians and hospitals to self-report healthcare-associated infections, and this leads to the paradox that hospitals that do the worst job of collecting data and documenting infections report the lowest rates.
External Validity (Generalizability)
The sections above on bias and errors concern internal validity; that is, are we measuring correctly within the population we selected? External validity or generalizability asks the question, are our results applicable in other settings? Generalizability is always a matter of opinion. A lack of bias does not guarantee generalizability. A perfectly done epidemiologic study may or may not be generalizable to a larger population.
Epidemiologists frequently choose to study unrepresentative samples of subjects in order to answer a scientific question cleanly, cheaply, practically, or safely. Although not widely generalizable, a study result may be scientifically sound for the population on which the study was performed. In a randomized trial, for example, potential study subjects and their physicians must determine that it is safe for the study subjects to accept any of the study treatments before they can be randomized. Patients who have a contraindication to one of the treatments cannot be included in the study on the chance that they might be randomized to the contraindicated treatment. Thus, many treatable patients must ordinarily be excluded from randomized trials, rendering the sample of patients on whom the trial is actually performed highly unrepresentative of the population as a whole (17). This lack of representativeness does not indicate that the study is epidemiologically biased, but it may limit the generalizability of the study result to a larger population.
The Collaborative Antibiotic Prophylaxis Efficacy Research Study (CAPERS) of antibiotic prophylaxis for clean (herniorrhaphy and breast) surgery used both experimental and observational components (18,19). In the experimental component, 1,218 patients were randomized to receive or not receive prophylaxis; patients were not included in this study if they or their physicians did not provide consent. In the observational component, 3,202 other patients received prophylaxis at the discretion of their surgeons. Both components showed that about half of the SSIs were prevented by antibiotic prophylaxis. In this particular instance, the result of the randomized trial turned out to be generalizable to the larger group, but this need not have been so.
ACCOUNTING FOR TIME AT RISK
Because many healthcare-associated infections are related to time at risk, and because average lengths of hospital stay are decreasing, state-of-the-art studies must use methods that account for time at risk. Studies of mortality present a similar challenge: we all have one death per lifetime, and that is unavoidable, but it matters very much just when that death occurs. Methods used to account for time at risk include incidence density methods and survival analysis.
Incidence Density
Incidence density studies are a type of cohort study where the denominator is the total person-time at risk for all subjects, rather than the number of subjects. Commonly used denominators in healthcare-related incidence density studies are patient-days (vascular or urinary), catheter-days, and ventilator-days. Of the four most commonly studied healthcare-associated infections, three are device-related and are best studied using incidence density methods: catheter-associated bloodstream infections (BSIs), ventilator-associated pneumonias, and catheter-associated urinary tract infections (20).
Only one of the four (SSI) is best studied using cumulative incidence methods; that is, the denominator is the number of surgical procedures.
Only one of the four (SSI) is best studied using cumulative incidence methods; that is, the denominator is the number of surgical procedures.
If the event being studied is an infection, then incidence density is the number of infections in a specified quantity of person-time in the population at risk. The population at risk is composed of all those who have not yet suffered an infection. After a patient acquires an infection, that patient would be withdrawn from the population at risk. All hospital days for each patient who never acquired an infection would be included in the pool of days at risk, but for a patient who became infected only those hospital-days before the onset of the infection would be included.
Incidence density is the instantaneous rate of change or what used to be called the force of morbidity. For convenience in healthcare epidemiology, healthcare-associated infection rates are usually expressed as the number of events in 1,000 hospital-days, because this usually produces a small single- or double-digit number, but we could have used seconds or years.
The basic value of this measure can be seen when comparing healthcare-associated infection rates in two groups with large differences in time at risk, for example, in short-stay patients versus long-stay patients, or infection rates with peripheral venous catheters versus implanted ports. By contrast, if one looks at events that come from a point source, such as eating vanilla ice cream at a church supper, or events that are not time related, like acquiring tuberculosis during bronchoscopy with a contaminated bronchoscope, the attack rate or cumulative incidence is an excellent measure of incidence. SSIs are usually thought of as having a point source—the operation; therefore, cumulative incidence methods are adequate for studies of SSI.
An incidence density rate = total events/total time at risk for an event. If we have an exposed and nonexposed group, then we define the rate ratio = rate ill in exposed/rate ill in nonexposed. The rate ratio is a measure of the size of effect analogous to the relative risk used in cumulative incidence studies. Rate ratios are sometimes called incidence density ratios, relative risks, or risk ratios. Rate ratios are interpreted in a similar manner to relative risks; a rate ratio of 2 means that disease incidence was twice as great in the exposed group than in the nonexposed group. Note that the units for the denominators of incidence density divide out, so that you will find the same incidence density ratio no matter whether you use time units of seconds or millennia. P values for the rate ratio may be calculated by a chi-square or binomial exact method.
Multiple Events in a Single Patient
Standard statistical tests assume that each observation in a data set is independent, having no linkage with other observations. A corollary is that each subject in a study should contribute at most one event to a data set; that is, we should study only first events in an individual. If this rule is not followed, the calculated confidence intervals and p values may not be valid. However, it is well-known that a subset of patients will have multiple episodes of infection and other adverse outcomes. Also, patients with a first event are more likely to suffer a second (21,22,23,24,25). For quantitative analyses, these nonindependent events cannot simply be summed. The biologic and statistical import of 5 infections per 100 discharges would be entirely different depending on whether it represented five sequential infections in a single patient or five first infections in 5 different patients.
Furthermore, a first healthcare-associated infection becomes a risk factor for a second, and risk factors for multiple infections are different from the risk factors for a first infection. The simplest way to cope with multiple incident events in the same individual is to restrict quantitative analyses to first events. A second method is to stratify by number of previous infections, for example, study the effect of exposures on risk of first infection, then on risk of second infection, and so on. These individual strata would then be combined into a summary relative risk. However, this method also violates the independence rule for conventional data analyses. A third alternative is to use statistical methods designed for longitudinal or correlated data. This type of analysis is technically complex (see Longitudinal Analysis and Repeated Measures, below).
Survival Analysis
Survival analysis is a second method for accounting for time at risk (3). Survival analysis usually consists of the familiar Kaplan-Meier plot, where at time zero survival begins at 1.0 or 100% and gradually falls off as subjects are followed forward in time. Survival can literally mean not dying, or it can mean remaining free of infection or whatever outcome variable is being studied. The opposite of survival is termed “failure,” which again may either mean death or onset of another adverse event. An extremely useful feature of survival analysis is that it can make use of subjects who are lost to follow-up or die of a disease other than that of interest; these subjects are called “censored” since we don’t know if they would have failed if we had been able to follow them for a longer period of time.
Statistical packages automatically plot survival curves for two or more groups and calculate a p value for the difference between the two groups. Median survival (the follow-up time when the probability of survival is 0.5 or 50%) is often reported. The Kaplan-Meier plot represents a univariable analysis. Multivariable survival analysis is accomplished via regression models, the most common of which is the Cox model (discussed below).
CONFOUNDING AND EFFECT MODIFICATION
Confounding
Confounding can be defined as “a situation in which a measure of the effect of an exposure on risk is distorted because of the association of the exposure with other factor(s) that influence the outcome under study” (1). An intuitive example given in the chapter introduction was “our infection rate is higher than theirs because our patients are sicker than theirs.” We can set up an experimental study to measure the effect of only one exposure at a time, but in observational studies where several exposures may act jointly to produce disease, we often need to use statistical techniques to tease out the independent effect of any one exposure.
TABLE 2-3 Sample Data: Simple and Stratified Analyses | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
