The practice of medicine is an art, performed for the healing and reduction in suffering of individual patients. Doctors practice their art through skilled application of available medical knowledge. Before the scientific and technological advances made in the last century, medical knowledge belonged to a select few and was passed from teachers to students as if from parents to children (see the first point in the Hippocratic Oath) (1). Although much had been learned through careful observation of human anatomy and disease, empirical evidence on prognoses and treatment outcomes was limited. Rational treatment decisions could be made deductively or on the basis of accepted beliefs; however, the inability to obtain extensive empirical evidence left the value of many treatments unproven and poorly understood.

Modern medical researchers have applied the scientific method and taken advantage of advances in information technology to produce an ever-expanding body of evidence useful in medical decision making. The scientific method (construction of a hypothesis, design of an experiment, analysis of the data, and communication of the results) and the ability to collect and analyze large amounts of data enable researchers to study the comparative effects of different therapeutic approaches. Opinions on the best treatment for a specific condition are often considered to be hypotheses and tested in clinical studies. Application of statistical methods to data from large populations of patients provides the ability to estimate the average response to treatment, along with the variation in response among patients, and statistical models can be used to identify factors associated with better or poorer response.

The art of medicine has been greatly expanded through the use of evidence-based methods. Multidisciplinary teams design, implement, analyze, and interpret the clinical studies that collectively form the body of evidence. Modern scientific principles require study reports to be publicly available and subject to scrutiny, often leading to debate about the appropriate interpretation of the results. Assessment of the validity of study results requires consideration of important factors such as the method of data collection and cleaning, relevance of the study patients to those seen in actual practice, methods for minimization of bias, and even the motivation of the investigators. Views about the best treatment are routinely examined in light of shared evidence, which is used to develop guidelines to aid in medical decision making. Modern physicians must have the ability to understand and interpret evidence and to make appropriate changes in their practice in light of new findings.

The clinical perspective, focusing on a single patient, is now balanced by the statistical perspective, which makes inferences from populations. It is important to keep in mind that response to a therapy can vary from one patient to the next, and the results from a single patient therefore do not necessarily generalize to an entire group. For the same reason, results from a population do not accurately predict what will happen to each patient in the population. The goal of evidence-based medicine is to provide physicians with the best available information to make individual treatment decisions. This is accomplished by joining the clinical and statistical perspectives to identify approaches that produce the best outcomes for the most patients.

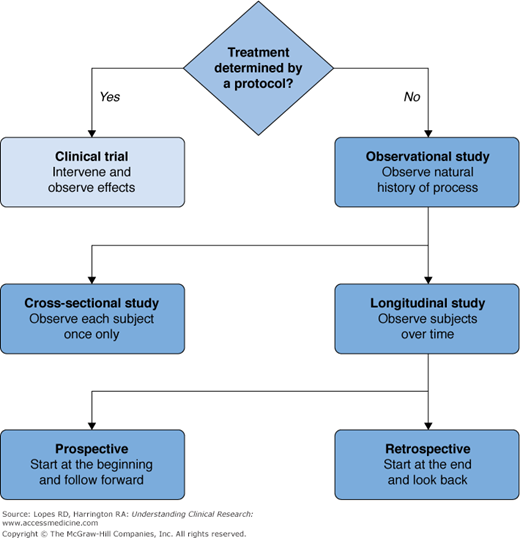
A clinical study is any attempt to learn more about a disease and its manifestations, causes, or outcomes. Clinical studies range in size from small, such as descriptions of a few interesting cases, to large, including many thousands of patients. Larger studies involve construction of a database and the use of sophisticated statistical methods to analyze the data. Retrospective studies collect and analyze data from events that have already occurred. Prospective studies identify a population of subjects (cohort) and follow them into the future from a specified time point, collecting data on events that occur as time passes. Our focus will be on a specific type of prospective study, the clinical trial, which has become the accepted best method for investigating the effects of medical treatments and the fundamental tool in the clinical development of new therapies (see Figure 5–1).

A clinical trial is a study in humans that evaluates the effects of a specific medical or health-related intervention. Clinical trials that produce the most reliable results have three important characteristics: (1) a quantifiable and relevant outcome, (2) the existence of a control group, and (3) treatment assignment determined by a protocol. This third characteristic implicitly requires a clinical trial to be prospective.

The quantifiable outcome in a clinical trial may be as simple as “Did the patient get better? 0 = no, 1 = yes.” Or the outcome might involve a straightforward calculation such as “change in diastolic blood pressure from baseline after 2 weeks of treatment.” It is not unusual for outcomes to be more complex, such as “time from randomization to cardiovascular death or hospitalization for cardiovascular causes, whichever occurs first.”

In addition to being quantifiable, an outcome should also be a relevant measure of the severity or extent of the disease being studied, so that changes in the outcome are associated with changes in symptoms or signs of the disease. Relevancy of outcome measures, also known as content validity, should be a major consideration in both the design and interpretation of clinical trials.

The basis for inference from a clinical trial is the observed difference in the summarized outcome measure(s) between a group that received an experimental treatment and a group that received the control treatment, such as a placebo or no treatment at all. This difference is the observed treatment effect. The main analysis of a clinical trial reports the observed treatment effect for an outcome along with a statement about the probability of seeing an effect of similar or greater magnitude if the control and experimental treatments truly were not different. Treatment effect is most easily understood when it is represented by the difference between two means; however, it is quite common for the effect to be expressed as a ratio, such as the relative risk of a negative outcome. The calculation of an observed treatment effect can be somewhat complex; for example, in a stratified analysis, the effect is calculated separately for different subgroups of patients and then combined across the subgroups. Stratified analyses can produce more precise or accurate estimates of treatment effect and also provide the ability to test for homogeneity of the effect in different subgroups of patients. Commonly used stratification factors are sex, age, and race as well as known measures of risk observable at baseline. Even when study designs or analyses appear complicated, the treatment effect is fundamentally the difference between the experimental and control groups. Reliable estimation of the treatment effect requires a valid control group.

Assignment of treatment by a protocol reduces the chance that investigators might introduce bias by (consciously or subconsciously) selecting different types of patients for the experimental and control arms, thereby building in a difference between treatment arms that reflects factors unrelated to treatment. Randomization is the preferred method for avoiding bias in treatment assignment, because it assures that the treatment a patient will receive is determined by chance and is therefore unrelated to characteristics of the specific patient. Whenever possible it is advantageous to ensure that investigators and patients are unaware of which treatment is received. This technique, called blinding, makes it unlikely that treatment assignment for a new patient could be accurately predicted, and it also reduces the potential for bias in the reporting of measurements taken during the study.

The importance of requiring treatment assignment to be done by a protocol is seen in the example of an hypothetical retrospective study comparing myocardial infarction-free survival between patients who chose surgical intervention for single-vessel ischemic heart disease and patients who chose medical therapy. Comparisons between the surgical and medical groups might be confounded if patients who chose surgery tended to have a different baseline risk of negative outcome compared with patients who chose medical therapy. Statistical techniques could adjust the comparison to account for differences between the surgical and medical groups; however, the validity of the adjustments would depend on the completeness of information on baseline risk of the patients in the study. Stronger evidence on the relative efficacy of surgery and medical treatment could be obtained from a prospective study employing random assignment to treatment.

In the classical clinical trial, two treatments—control (C) and test (T)—are compared on the basis of a quantifiable outcome measure. We wish to know whether the test treatment is better than the control treatment, and the trial will have one of two conclusions. Either the test treatment will be proven to be better than the control (trial is positive) or it will not (trial is negative). Studies designed this way are called superiority trials, because the goal is to show that T is better than C. We assume that the means for groups C and T, μC and μT, represent the true averages of the outcome variable among all patients eligible to receive C or T. “Mean” in this context stands for a statistical measure of central tendency that summarizes the outcome in a group. The true treatment effect is Δ = μT – μC, the difference between the average test group and control group outcomes.

To set up the mechanism for inference, we assume that there is no difference between the test and the control, that is, Δ = 0. This is called the null hypothesis. If the null hypothesis is true, then we would expect that the results from the trial would produce an observed Δ approximately equal to 0. In a positive trial, the observed Δ would be so different from 0 that we would not believe that the null hypothesis could be true. In this case, we would reject the null hypothesis and claim that there is indeed a treatment effect. If the observed Δ is not far enough from 0 to convince us that the treatments are different, then we have a negative trial, or a failure to reject the null hypothesis.

It is important to consider the possibility of making a wrong decision from a clinical trial. One kind of wrong decision would be made if we claimed that the test treatment was better than the control, when in fact it was not. This would be a Type I error or false positive. The other kind of wrong decision would be made if we claimed that the test was not better than the control, when in fact it really was. This would be a Type II error or false negative (Table 5–1). The sizes of Type I error (α) and Type II error (β) are specified in the design of the study and are important determinants of the sample size.

The ways that we control for Type I and II errors are conceptually different. This can be seen by examining how a test statistic determines whether a trial is positive or negative. A test statistic can be thought of as a ratio of the difference between the observed average outcomes (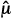T – 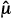C) in the test and control arms and the standard deviation, sdiff, of this difference. (For some types of data and statistical tests, more complicated formulations for the test statistic might be used.) A test statistic (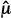T – 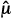C)/sdiff is like a signal-to-noise ratio; the ratio is increased by a larger signal (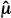T – 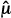C) and decreased by greater noise (sdiff). Statistical significance is reported when the computed test statistic is so large that, if the test and control arms were not really different and we were to repeat our clinical trial many times, no more than 100 × α% of the repeats would produce a test statistic as large as the one we observed. The P value is the computed probability of observing a test statistic at least as large as the one we observed, assuming the null hypothesis of no difference between the treatment arms. Statistical significance is claimed if the P value is less than the prespecified α. In most positive trials, the P value will be considerably lower than α. (Not to be confused with statistical significance is clinical significance

Stay updated, free articles. Join our Telegram channel

Join