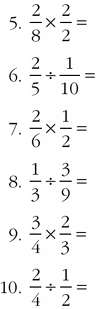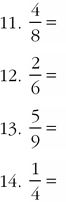Arithmetic Review

Preventing Medication Errors

Every nurse must know and practice the six rights of medication administration including the

Right drug
Right dose
Right route
Right time
Right patient
Right documentation

Although the right drug, route, time, patient, and documentation may be readily identified, the right dose requires arithmetic skills that may be difficult for you. This chapter reviews the basic arithmetic skills (multiplication and division) necessary for calculating medication dosage problems using the problem-solving method of dimensional analysis. Calculating the right dose of medication to be administered to a patient is one of the first steps toward preventing medication errors.

Arabic Numbers and Roman Numerals

Most medication dosages are ordered by the physician or the nurse practitioner in the metric and household systems for weights and measures using the Arabic number system with symbols called digits (ie, 1, 2, 3, 4, 5). Occasionally, orders are received in the apothecaries’ system of weights and measures using the Roman numeral system with numbers represented by symbols (ie, I, V, X). The Roman numeral system uses seven basic symbols, and various combinations of these symbols represent all numbers in the Arabic number system.

Table 1.1 includes the seven basic Roman numerals and the corresponding Arabic numbers.

The combination of Roman numeral symbols is based on three specific principles:

Preventing Medication Errors

Correctly identifying Roman numerals will assist in preventing medication errors. Some medication orders may include a Roman numeral.

Example: Administer X gr of aspirin, which is correctly interpreted as administer 10 gr of aspirin.

However, according to the Institute for Safe Medication Practices (ISMP), abbreviations increase the risk of medication errors. Additionally, while some health care providers may still use roman numerals and the apothecaries’ system, the ISMP recommends using the metric system.

1. Symbols are used to construct a number, but no symbol may be used more than three times. The exception is the symbol for five (V), which is used only once because there is a symbol for 10 (X) and a combination of symbols for 15 (XV).

2. When symbols of lesser value follow symbols of greater value, they are added to construct a number.

3. When symbols of greater value follow symbols of lesser value, those of lesser value are subtracted from those of higher value to construct a number.

Table 1.1 Seven Basic Roman Numerals

Roman Numerals	Arabic Numbers
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

Exercise 1.1 Arabic Numbers and Roman Numerals (See page 23 for answers)

Express the following Arabic numbers as Roman numerals.

1. 1 = ______
2. 2 = ______
3. 3 = ______
4. 4 = ______
5. 5 = ______
6. 6 = ______
7. 7 = ______
8. 8 = ______
9. 9 = ______
10. 10 = ______
11. 11 = ______
12. 12 = ______
13. 13 = ______
14. 14 = ______
15. 15 = ______
16. 16 = ______
17. 17 = ______
18. 18 = ______
19. 19 = ______
20. 20 = ______

Although medication orders rarely involve Roman numerals higher than 20, for additional practice, express the following Arabic numbers as Roman numerals.

21. 43 = ______
22. 24 = ______
23. 55 = ______
24. 32 = ______
25. 102 = ______
26. 150 = ______
27. 75 = ______
28. 92 = ______
29. 64 = ______
30. 69 = ______

Express the following Roman numerals as Arabic numbers.

31. II = ______
32. IV = ______
33. VI = ______
34. X = ______
35. VIII = ______
36. XIX = ______
37. XX = ______
38. XVIII = ______
39. I = ______
40. XV = ______
41. III = ______
42. V = ______
43. IX = ______
44. VII = ______
45. XI = ______
46. XIV = ______
47. XVI = ______
48. XII = ______
49. XVII = ______
50. XIII = ______

To increase your abilities to use either system, convert the following Arabic numbers or Roman numerals.

51. 19 = ______
52. XII = ______
53. 7 = ______
54. IX = ______
55. IV = ______
56. 11 = ______
57. VIII = ______
58. 16 = ______
59. XX = ______
60. 5 = ______
61. I = ______
62. 18 = ______
63. VI = ______
64. 2 = ______
65. III = ______
66. 10 = ______
67. XIII = ______
68. 14 = ______
69. XV = ______
70. 17 = ______

Fractions

Medication dosages with fractions are occasionally ordered by the physician or used by the pharmaceutical manufacturer on the drug label. A fraction is a number that represents part of a whole number and contains three parts:

Numerator—the number on the top portion of the fraction that represents the number of parts of the whole fraction.
Dividing line—the line separating the top portion of the fraction from the bottom portion of the fraction.
Denominator—the number on the bottom portion of the fraction that represents the number of parts into which the whole is divided.

To solve medication dosage calculation problems using dimensional analysis, you must be able to identify the numerator and denominator portion of the problem. You also must be able to multiply and divide numbers, fractions, and decimals.

Multiplying Fractions

The three steps for multiplying fractions are: