Collecting Evidence for Medical Practice
Clinical Trials 7
HEALTH SCENARIO
Stroke is a potentially debilitating medical event that affects approximately 800,000 people in the United States each year, leaving as many as 30% of survivors permanently disabled. Given this impact, there is great demand for treatments that significantly improve functional outcome after a stroke. To date, few clinical trials for the treatment of acute stroke have succeeded. Suppose you and a team of collaborators have a new treatment that you would like to test for use in patients who have had strokes. Where do you begin? How many patients do you need to sample to know if your treatment is safe and effective? How do you choose a comparison group and allocate treatment? How do you choose the outcome of interest and conduct the analysis of your data? These questions will be addressed in the following sections.
INTRODUCTION
A clinical trial is a prospective research study conducted in humans to assess the impact of an experimental intervention. The intervention can be a drug product, a device such as a surgical stent or diagnostic tool, a procedure such as a surgical treatment, or a behavioral intervention. Clinical trials are a critical step to therapeutic development because they provide the necessary methodology to make inferences with minimal bias and the best possible precision. Clinical trials have been in existence since the 1700s, although the primary concepts and terminology of trials were not identified until much later (Figure 7-1, Timeline), and clinical trial methods and regulations continue to be developed.
Figure 7-1. Clinical trial history. CE, Comparative Effectiveness; CFR, Code of Federal Regulations; CONSORT, Consolidated Standards of Reporting Trials; FDA, Food and Drug Administration; GCP, Good Clinical Practice; ICH, International Conference on Harmonization; IRB, Institutional Review Board; NCI, National Cancer Institute; NIH, National Institutes of Health; SCT, Society for Clinical Trials.
The history of clinical trials is important for understanding the impetus for good clinical practice guidelines, as well as the evolution of the drug and device development process. On average, the typical time from initial development to introduction into clinical practice for a drug in the United States is 15 years (Woosley and Cossman, 2007). Because therapeutic development is a time-consuming and costly process, it is important to take the time to develop the most appropriate study design and ensure proper conduct and analysis of the trial. There are plenty of examples of failed clinical trials, and the cause is not necessarily the absence of a treatment effect. For example, several trials were conducted in acute stroke only to conclude that patients may not have been treated early enough after the injury. Similarly, hundreds of AIDS trials were conducted before it was determined that CD4 cell levels might not be a reliable surrogate for AIDS. There are examples in areas where technology is evolving quickly in which the intervention under study becomes outdated by the end of the trial. Some of these failures can be avoided with the appropriate trial design.
A successful trial depends not only on the right design but also on the right team. Clinical trials demand a team approach, which includes, at a minimum, the clinical researcher, biostatistician, study coordinator, and patients. This chapter provides an introductory view of clinical trials, including study design, study population, randomization and blinding methods, sample size estimation, and outcomes and analyses.
CLINICAL TRIAL DESIGNS
There are a variety of clinical trial designs. The best design for any specific study depends on a number of issues, including the research question to be addressed, the type of treatment under investigation, and characteristics of the patient population being studied. Although we often think of clinical trials as a method for investigating new therapeutic interventions, clinical trials can also investigate prevention strategies, screening and diagnostic efforts, or supportive care designed to lessen symptom severity and improve quality of life rather than to cure disease.
Sound scientific clinical investigation almost always requires that a control group be used against which the experimental intervention can be compared. To control for expectations and some of the “nonspecific” therapeutic benefit of contact with professionals, many medication trials use a placebo, a biologically inactive substance that is identical in appearance to the medication under investigation. In trials of therapeutic devices, there is usually some attempt made to mimic the device application while not delivering the therapeutic elements of treatment (e.g., sham transcranial magnetic stimulation in which the device is applied but no current is delivered). In some disease states, the use of a placebo is considered unethical because there are known efficacious therapies and to deny a participant access to these treatments places them at unnecessary risk for harm. In these cases, an active control group receiving an existing standard treatment typically is used.
As recently as 50 years ago, the primary means of evaluating a new treatment was to compare a group of individuals treated with the new method to outcomes observed in the past from a group of individuals who received standard therapy, referred to as “historical controls.” There are several problems inherent in this approach. The primary problem is that it does not allow the investigator to control for the effects of important potential prognostic characteristics of the groups over time (e.g., age, sex, socioeconomic factors). In addition, there could be important variations in the disease state depending on seasonal variation, changes in environmental determinants, and so on over time. In addition, diagnostic criteria and sensitivity of methods for diagnosis of various disease states may change over time, making historical controls a less valid comparison group. For example, improved detection methods may result in earlier stage, more treatable extent of disease than existed historically.
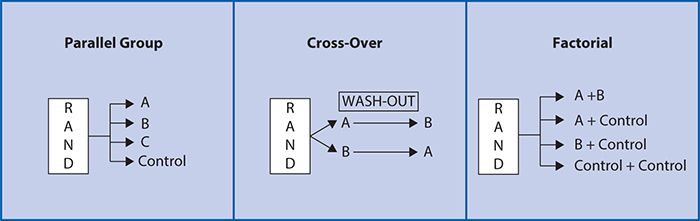
As such, a randomized, controlled clinical trial is often considered to be the “gold standard” for testing a new medication or therapeutic device. Other common designs include pre-/post-, crossover and factorial (Figure 7-2). These are generally conducted using a parallel group design in which two or more treatment groups are treated at approximately the same time and directly compared (Figure 7-2). In a pre-post comparison study design, individuals serve as their own controls with a basic comparison made before and after treatment. In a cross-over study design, each participant also serves as his or her own control, but subjects are randomized to sequences of treatments. For example, at random, half of subjects receive treatment A followed by treatment B, and the other half at random receive treatment B followed by treatment A. Varying the order in which the subjects receive the treatment allows for investigation of whether there is any impact of the order in which the treatments are delivered on the treatment outcome. A “wash-out” period or time between treatment periods is also often used to minimize the likelihood that the treatment in the first period will impact the outcomes of the treatment in the second period (“carry-over effect”). A cross-over design study can have more than two treatment periods. There are several advantages to the cross-over design. Because each subject is used as his or her own control, the treatment comparison has only within-subject variability compared with between-subject variability, allowing a smaller sample size to be studied. There are, however, a number of disadvantages. It is most suitable for studying chronic conditions (e.g., diabetes mellitus) that can be expected to return to a baseline level of severity at the beginning of the second treatment period and is not a suitable design for the study of any disease states that may be cured during the first treatment period (e.g., many acute infections). In addition, the assumption that the effects of intervention during the first period will not carry over into subsequent periods must be valid. In addition, subject drop-out (i.e., voluntarily or involuntarily discontinuing participation) before the second treatment period can severely limit the validity of the results.
Figure 7-2. Study design examples.
The factorial design (Figure 7-2) attempts to evaluate two interventions compared with a control within a single trial. Given the cost and effort involved in recruitment for clinical trials, this is an efficient and attractive proposition. If it can be validly assumed that there is no interaction between the two interventions being compared, with only a modest increase in sample size, two experiments can be conducted simultaneously. However, one concern with factorial design is the possibility of an interaction between the two interventions being compared. An interaction exists when the two treatments administered together have a greater effect than would be expected from the combination of the separate effects of the treatments when administered individually. An interaction may arise when the two treatments impact on different biological processes, thereby amplifying each other’s effect. When interaction is present, the sample size must be increased to account for the interaction. As such, the factorial design can be particularly appropriate and efficient either when there is no interaction expected or when the interaction between two treatments is an important focus of the study.
Other types of designs include cluster randomized trials, equivalence trials and adaptive trials. These designs address a specific study setting as described herein. In group allocation or cluster randomization designs, a group of individuals (e.g., those attending a clinic, school, or community) is randomized to a particular intervention or control. In this type of design, the basic sampling unit is the group, not individual participants, and the overall sample size needs be inflated accordingly. Cluster randomized designs are a good option when one is concerned with contamination across treatment groups. For example, a trial on a new educational program should be concerned with contamination (those not intended to have the experimental treatment receiving it inadvertently because of proximity and sharing with the experimental subjects) within the same school or same grades. Therefore, one would consider randomizing by grades or schools rather than by individual students.
In studies of equivalency, or noninferiority trials, the objective is to test whether a new intervention is as good as or no worse than an established one. The control or standard therapy in such a trial must have established efficacy. The investigator must specify what is meant by equivalence because it cannot be proven that two therapies have absolutely identical effects, as an infinite sample size would be required to prove equivalence. In this situation, outcomes other than the primary become important as frequency, and severity of adverse events (AEs), quality of life measures, ease of use, and costs may be important secondary bases of comparison in preferring one treatment over another.
An adaptive design allows predefined design adaptations to be made to trial procedures of ongoing clinical trials. In adaptive trials, as the trial progresses, the collected data are used to guide the predefined adaptation of the trial during its progress. The adaptations can be to drop a treatment arm that is not effective, alter dose levels, or increase the trial size if pretrial assumptions are not as predicted. This means that the dosing, eligibility criteria, sample size, or treatment settings can be adjusted during the course of the trial as evidence accumulates. The most important aspect of these designs is that the adaptations must be defined before the onset of the trial so that the statistical team can assess the impact of the changes on trial operating characteristics such as sample size and the possibility of a false conclusion. Adaptive designs have the potential to accelerate therapeutic development, but there are methodologic and implementation challenges in terms of randomization and statistical analysis that are specific to adaptive design clinical trials.
One of the motivations for conducting clinical trials is the persistent and unexplained variability in clinical practice (see Chapter 16) and high rates of care for which evidence of effectiveness is lacking (see Chapter 11). The increasing cost of health care has fueled an increasing demand for evidence of clinical effectiveness (see Chapter 11). Clinical trials that are developed specifically to answer the questions faced by clinical decision makers are called pragmatic or practical clinical trials (PCTs). PCTs often address practical questions about the risks, benefits, and costs of interventions as would occur in routine clinical practice. In general, PCTs focus on a relatively easily administered intervention and an easily ascertained outcome. Characteristic features of PCTs are that they compare clinically relevant alternative interventions, include a diverse population of study participants, recruit from heterogeneous practice settings, and collect data on a broad range of health outcomes (Tunis et al., 2003).
CLINICAL TRIAL PHASES
Clinical studies conducted to evaluate the therapeutic potential of a compound for a given illness have been divided into four phases. Before clinical studies, one often begins with translational research that brings the laboratory bench science and preclinical studies to the bedside so that new interventions (e.g., drugs, devices, behavioral interventions) can be further studied to develop promising new treatments. Clinical studies generally begin cautiously. As experience with the agent grows, the questions expand from tolerable dose to safety and then to efficacy. The number of subjects studied at each phase and the duration of studies can vary significantly depending on statistical considerations, the prevalence of the disease under consideration, and the agent under investigation. There are, however, some general principles and procedures regarding the four phases of clinical testing described below.
Phase I Clinical Trials
In phase I trials, the compound under investigation is administered to humans for the first time. Phase I studies generally are conducted in a hospital setting with close medical monitoring. When possible, phase I studies are conducted in normal, healthy volunteers to allow for the evaluation of the effects of the drug in a subject with no preexisting disease conditions. In some situations when it is not ethical to use normal human volunteers (e.g., testing oncology drugs, which are highly toxic), testing may be done in volunteers who have the disorder under investigation and have exhausted all other available treatment options.
The purpose of a phase I trial is to determine basic safety, pharmacokinetic, and pharmacologic information. These studies generally share certain characteristics. A series of ascending dose levels is used, with initial doses determined by extrapolation from animal data, beginning with a low dose and proceeding until a dose range suitable for use in later trials is identified. A small group of subjects is treated concurrently and may receive one dose of medication or several doses in a series of consecutive treatment periods. Data from each set of studies are generally collected and assessed before choosing the next set of doses for administration. Adverse Events (AEs) are investigated intensively in phase I trials. In some cases, such as the investigation of oncology drugs, dose escalation is continued until limited by toxicity for the determination of a maximally tolerated dose (MTD). Although clinical monitoring for AEs is one of the critical elements of all first-in-human studies, the MTD is not the universal endpoint of phase I investigation, and when appropriate, the endpoint for dose escalation may be a given plasma concentration or a biomarker for some indication of the action for the agent (Collins, 2000).
A diversity of procedures can be used in phase I trials. For many compounds, it is anticipated that AEs will not be a major limiting concern. In this case, AEs are monitored, but the principal observations of interest are pharmacokinetic and pharmacodynamic endpoints. Parameters repeatedly assessed during most phase I trials include vital signs, physical and neurologic status, laboratory testing (in particular hepatic, renal, hematopoietic function), cardiac conduction (serial electrocardiography [ECG] or telemetry), and AEs. Pharmacokinetic parameters after single, repeated, and a range of doses are assessed. Assessments include maximal plasma concentrations, time to maximal plasma concentration, time to steady state, elimination half-life, plasma accumulation, and total drug exposure to test for dose-plasma level proportionality. Studies investigating bioavailability, particularly by the oral route of administration, food effects on absorption, and relative bioavailability studies of different formulations (e.g., capsule and solution), are also conducted. The metabolic profile and elimination pathways also are determined.
Phase II Clinical Trials
Phase II clinical trials range from small, single-arm studies to randomized trials comparing a control treatment with the experimental drug in either a single dose or at several doses. Because these studies vary considerably in size and study objectives, the study designs are quite heterogeneous. In phase II studies, the study subjects are the patient population that has the disorder of interest. There is an assessment of treatment efficacy as well as safety. Phase II trials are designed to extend the safety database and provide initial evidence for efficacy of the compound. Phase II trials are not designed to give definitive evidence of efficacy, and the goal of the trial is to lead to a decision concerning further (phase III) testing rather than regulatory submission. Although the focus of a phase II study is efficacy, further information about drug delivery, protocol feasibility, dosing, and AEs are gathered. As in phase I, data collected may include pharmacokinetics, repeated physical and neurologic examinations, comprehensive laboratory testing, cardiac conduction (ECG), and vital signs. The primary outcome variables typically are focused on the target condition. These usually include relevant illness appropriate rating scales such as the Clinical Global Impression (CGI) rating for mental health studies, the modified Rankin scale (mRS) for stroke, and so forth. There is an emphasis on adverse effects and compliance, usually determined by both pill count and pharmacokinetic parameters. Frequency of visits depends on the target condition and the agent under investigation. There may be a required period of “in-clinic,” close medical assessment after administration of the initial dose(s) of the compound in situations when there are some acute effects of concern.
Phase III Clinical Trials
Phase III trials are large clinical studies that can involve the treatment of several hundred subjects from multiple centers with a goal of assessing therapeutic benefit. The large number of patients involved allows for the development of a broad database of information about the safety and efficacy of the drug candidate. Despite the large numbers of patients studied, the exclusion criteria for phase III trials are stringent. As in phase II trials, subjects with comorbid conditions other than the target condition under investigation generally are excluded.
Study designs used in phase III trials are less heterogeneous than those used in phase II because of the need to meet defined regulatory standards for the New Drug Application (NDA) to the Food and Drug Administration (FDA). The study duration is variable depending on the therapeutic area. The assessments of laboratory data and physical and neurologic examination are less frequent than in the phase I and II trials and outcome measures generally include assessment of the primary outcome (target condition) using disease-specific measures (e.g., reducing symptoms, arresting or reversing an underlying pathologic process, decreasing complications of the illness) and secondary outcome measures such as quality of life and disability measures.
Phase III trials often include fixed-dose studies, flexible dose studies, and studies that include the comparison of a “gold standard” treatment along with the experimental agent and placebo. The large group of geographically and demographically diverse participants may allow for the identification of rare AEs that only affect a few patients. Despite the earlier testing, approximately one in five potential drugs are eliminated during phase III of testing. However, if a drug candidate is successful in phase I and II, some of the phase III studies will be “pivotal” studies that will serve as the basis for FDA approval.
Phase IV Clinical Trials
Phase IV trials are initiated after a drug has been approved by the FDA. These trials are also referred to as postmarketing studies. They are generally conducted for the approved indication, but they may evaluate different doses, the effects of extended therapy, or the safety of the agent in patient populations that were not studied in the premarketing clinical trials. Phase IV trials may be initiated by the sponsor in an attempt to gather more information on the safety and efficacy of the drug, or they may be requested by the FDA. To evaluate the risk of rare side effects, phase IV trials often involve very large and diverse study populations.
STUDY PARTICIPANT SELECTION
The study population is a subset of individuals with the condition or characteristics of interest as defined by study eligibility criteria. The types of characteristics typically used for eligibility criteria include stage or severity of illness, age and gender of patients, absence of other comorbid conditions, and ease of follow-up. Careful consideration of study eligibility criteria is essential because it will impact the generalizability (extent to which results can be extrapolated to other patients) and utility of the study. In general, eligibility criteria are related to participant safety and the anticipated effect of the intervention. If the study population is very homogeneous with highly selective inclusion and exclusion criteria, the decreased variability in response means that a treatment effect is more likely to be detected if one truly exists. However, with a narrowly defined study population, the study results will not be as easily generalized to the entire universe of individuals with the disease state in question. However, if the study population is heterogeneous with few exclusion criteria, the variability in response may make it more difficult to discern a treatment effect, but the results of the study will have broad generalizability. It is of critical importance that the investigators give a careful and detailed description of the study population so that readers can fully assess the applicability of the findings to their patient populations. When defining the eligibility criteria, it is important to consider who will potentially benefit from the proposed experimental intervention, who will have minimal risk, and who will adhere to the intervention.
Choosing the right study population is important; however, it is just as important to ensure that certain populations are not neglected or coerced to participate and that there is an equitable selection of participants. For example, in the history of clinical research, it has been argued that women, children, and disadvantaged ethnic groups have either been harmfully neglected or exploited in clinical studies. These populations are referred to as vulnerable populations, a category of participants subject to an inequity in research. This category includes children, prisoners, pregnant women, disadvantaged ethnic groups, and persons with physical or mental disabilities. Great care should be taken when designing a clinical trial to ensure minimal risk to the participating population and equity in participant selection. This is why clinical research has a participant consent process referred to as the informed consent process. One main requirement when conducting a clinical trial is that all participants are fully informed about the trial. This includes understanding the intervention they may be given, what they will have to do if they take part in the trial, what benefit they might gain or what harm may come to them, what will happen to them after the trial is over, and what their rights may be to other treatments. When obtaining consent from minors or mentally impaired populations, there must be a person who is permitted to give consent on the participant’s behalf such as a parent or a legally authorized representative.
RANDOMIZATION AND BLINDING
Randomization of study participants is a key component of clinical trials with multiple treatment arms. The goal of randomization is to establish comparable groups with respect to both known and unknown prognostic factors, to minimize selection and accidental biases, and to ensure that appropriate statistical tests have valid significance levels. An important question regards how to randomize. Several randomization methods are available. Fixed allocation schemes, including simple randomization, blocked randomization, and stratified randomization, assign the intervention with a prespecified probability (equal or unequal) that remains constant during the study period. Simple randomization is analogous to flipping a coin when the rules are prespecified (e.g., heads = experimental; tails = control). Although easy to implement and provides random treatment assignment, simple randomization does not take into account important prognostic variables, so the balance of these variables across treatment arms is not guaranteed.
Constrained randomization, which includes blocked and stratified schemes, addresses this potential limitation of simple randomization. Using a blocked scheme, randomization is done within small subsets (small blocks). Block size is determined by the number of treatment arms and must be an exact integer multiple of the number of arms. For example, if a trial with two treatment arms has a chosen block size of four, then there are six possible permutations of treatments (ABAB, AABB, and so on). A list of blocks can be pregenerated, and when enrollment begins, blocks are randomly selected. It is important to completely fill a block before using another block because complete blocks ensure balance in treatment assignments. Although blocking does not ensure balance of important prognostic factors, this can be achieved by adding stratification. For example, if gender impacts the outcome of interest, the researcher should ensure that males and females receive equal treatment assignments. In a blocked stratified scheme, blocks would be set up within each stratum (i.e., male, female) to provide treatment assignment balance within each stratum. Although blocked, stratified schemes have been used commonly in trials (mainly because of their ease of implementation); there are cons to this approach. Specifically, one loses randomness in the assignment as a block fills, and the assignment becomes deterministic by the end of a block. As randomization methodologies expand, there are alternatives to fixed and constrained allocation schemes such as adaptive randomization schemes. Adaptive schemes allocate patients with a changing probability and include number adaptive, baseline adaptive, and response (outcome) adaptive. Although the various adaptive schemes can be more complex to implement, the advantages include minimized deterministic assignments and maintenance of the randomness of assignments. Schemes include minimization, minimal sufficient balance, and play the winner.
In addition to randomization, blinding, which means keeping the identity of treatment assignment hidden, is another important aspect of a clinical trial design. When the identity of treatment assignment is kept from the investigator and the evaluation team as well as the participant, this is referred to as a double-blind trial. Although not always feasible, blinding has several important features. It minimizes the potential biases resulting from differences in patient management, treatment, or interpretation of results and the influence of patient expectation, and it avoids subjective assessment and decisions that could occur if investigators or participants are aware of the treatment assignment.
Ideally, the participant, investigator, and evaluation team should be blinded to the treatment allocation, and it is important to ensure that the treatment assignment information remains confidential until the end of the trial. For example, if a participant is made aware that the next treatment assignment is to a placebo control arm, then he or she may decline participation, which may lead to a selection bias in the study population. If the investigator is made aware of the next treatment assignment, then he or she may decide to not enroll the next patient because of a specific patient characteristic such as disease severity, which also could produce selection bias. Similarly, if the various parties are blind to treatment allocation but are made aware after the assignment, then they may withdraw consent, or the care of that participant may be impacted if the evaluating team knows what intervention the patient received.
As previously mentioned, blinding is not always feasible. When considering the feasibility of blinding, ethics and practicality must be examined. The investigator needs to ensure that implementation of a blinding scheme will not result in harm to the participants. In terms of practicality, surgical trials, diagnostic studies, and behavioral studies often struggle with implementing blinding because the person delivering the intervention knows the assignment. Blinding of the allocation can still be maintained; however, at a minimum, the post-intervention evaluation should be done by a person(s) who is (are) blind to individual treatment assignment. This situation is often called a single-blind trial.
SAMPLE SIZE ESTIMATION
For every clinical trial, sample size must be determined to ensure adequate statistical power (ability to discern an effect, if present) for the proposed analysis plan. The question that is answered by sample size estimation is, “How many participants are needed in order to ensure a certain probability of detecting a clinically relevant difference at a defined significance level?” The overall goal of sample size estimation is to achieve reasonable precision in estimating the outcome of interest. That is to say, one should characterize the treatment effect within an acceptably narrow range of values consistent with the data. The study sample size should reflect what is needed to address the primary objective of the trial and the analysis of the outcome and should be enough to examine the secondary outcomes. Just as important, sample size needs to be determined so that a budget can be derived. The estimation of study sample size starts with the primary outcome. One needs to define the quantitative measure (outcome) and determine how to analyze it in order to estimate sample size. When there is a dichotomous (yes/no) outcome from a paired sample (McNemar test) but the sample size is estimated for an independent outcome (chi-square test), an incorrect sample size will be estimated and the trial is threatened to be underpowered to detect the relevant differences.
When calculating sample size, four parameters need to be predefined: the probability of a type I error, the probability of a type II error, the standard deviation of the outcome measure, and what you determine to be the clinically relevant difference between the experimental intervention and the control intervention. The type I error occurs when a null hypothesis is falsely rejected; for example, when testing to see if the experimental intervention is superior to the control intervention, a type I error occurs when there is a false claim of superiority. The probability of a type I error is referred to as the significance level of a test. Common values for a significant level are 0.05 or 0.10. A type II error occurs when one fails to reject the null hypothesis (e.g., in the superiority setting, this is falsely claiming no difference when in fact a true difference exists). Common values for type II error probabilities are 0.10 and 0.20. One minus type II error is the statistical power of the trial.
Clinical trials are concerned about power because the statistical power of the test tells us how likely we are to reject the null hypothesis given that the alternative hypothesis is true. If the power is too low (<80%), then we have insufficient chance of detecting the predefined clinically relevant difference. Invariably, the cause of low power is inadequate sample size. Just as important, though, is that we must acknowledge that statistical significance does not imply clinical significance. With unlimited funds, one could have a large enough study to have adequate power to detect a difference that is so small that it does not have any clinical meaning. For example, if one could afford to conduct a 10,000-patient trial and detected less than 1-point change in a continuous outcome scale, there is reason to doubt whether that 1-point change is clinically meaningful. Will the difference detected change practice? That is the most important question for the clinical researcher to bring to the table for sample size estimation.
The clinically relevant difference for trials is either defined as the absolute difference or the relative difference between the experimental treatment and control (i.e., how much difference should there be in order to change practice). In trials for acute spinal cord injury, the primary outcome is often the mean American Spinal Injury Association (ASIA) motor score at 12 months after randomization. When estimating sample size for a two-arm trial, we turn to the literature on the ASIA motor score for this population to guide us in determining the expected 12-month mean ASIA motor score for standard of care. If we assume that the control arm (standard of care) is going to have a mean score of 25 with a standard deviation of 15, then we need to determine what absolute difference should be detected in order to state the experimental treatment is beneficial compared with control. This is not an easy task and requires a combination of literature review, clinical expertise, and consensus. This is similar when the outcome is a proportion. Consider a trial with a primary outcome of proportion of successes in which success is defined by a certain predefined threshold of improvement. If we assume the proportion of successes in the population that is receiving the control is 30%, then how much better (e.g., 40%, 50%) does the proportion need to be in the experimental arm in order to claim it is better? This can be defined in absolute or relative terms. On an absolute scale, we can state that the experimental arm must have at least an absolute increase of 30%. We can take that same difference and turn it into a relative scale; the experimental arm must have a 50% relative increase in the success rate compared with the control. Both are acceptable approaches to defining the clinically relevant difference, but it is important to be clear which scale you are basing your sample size calculations on because you can get very different results if you mistakenly used the 50% absolute difference rather than the intended 30%.
OUTCOMES AND ANALYSIS
Research studies start with a question, which leads to study objectives, which lead to the definition of outcomes. Researchers often have multiple questions, and it is the responsibility of the study team to determine the primary versus the secondary and tertiary questions. The reason to delineate the major hypothesis is because in clinical trials, the primary question drives the various aspects of the study design, including sample size, study population, study procedures, and data analyses. Consider common questions in a clinical trial setting: What dose of a new experimental anticlotting drug is safe and well tolerated in patients with thrombotic strokes? Is an innovative surgical stenting procedure safe and effective in patients with carotid artery blockages? Is another new drug showing a signal of efficacy in preventing strokes in patients with transient ischemic attacks? These questions lead to objectives: to determine safety, to determine dose, and to determine efficacy. After one has the question and objectives, then one can determine the outcomes that need to be measured.
Outcomes, also referred to as endpoints, are the quantitative measures that correspond to the study objectives. The outcome can be continuous, categorical, ordinal, nominal, or a time to an event, or the outcome can be a composite measure. When choosing the study outcome, it is desirable for the outcome to have the following properties: valid and reliable, capable of being observed for every trial participant, free of measurement error, and clinically relevant. All of these properties are important, and the combination of the literature and the features of the disease that the intervention is targeting to improve should be used to help decide the best outcomes for the clinical trial. For example, in acute spinal cord injury trials, researchers examine mean ASIA motor scores to interpret treatment effects. For oncology trials, a common study outcome is a time to event such as overall survival or time to tumor progression. In acute stroke and cardiovascular disease trials, the outcome often is a proportion of good or bad outcomes as defined by dichotomizing the modified Rankin scale for stroke and reporting the proportion of nonfatal myocardial infarctions or the total mortality rate for cardiovascular disease. After the outcomes are defined, then one can consider the analysis plan.
If the primary outcome is a categorical variable, then an appropriate analysis for categorical outcomes must be used. For example, a simple dichotomous outcome (e.g., success or failure; yes or no) could be analyzed using a chi-square test. If a cell size is small, however, then the analysis may use Fisher’s exact test, or if data are not independent (e.g., each participant receives both treatment A and treatment B), then McNemar’s test for paired data should be used. Table 7-1 provides an example of how to display the data for a dichotomous outcome. When reporting results from a trial, it is very important to report both the point estimate of the treatment effect with the appropriate confidence interval (CI) and the P value produced from the statistical test. The CI includes the range of values that are consistent with the data observed at a defined level of statistical precision (e.g., 95%). This information will give the audience a more complete picture of the benefit of the experimental treatment. For example, based on the data in Table 7-1, we see that the experimental arm had 34 successes out of 141 randomized into that arm (proportion of success, pe, of 0.24), and the control arm had 25 successes out of 141 randomizations (pc = 0.18). The treatment effect of this trial can be reported as a 6% absolute risk difference (0.24 – 0.18) with a 95% CI of –3.1%, 15.8% between the proportion of success in the experimental arm compared with the control arm. This point estimate can be supported by conducting a chi-square test and reporting a test statistic of 1.74 and a P value of 0.19. Note that the 95% CI included the value of no effect (0% difference). This tells us that the point estimate of 6% difference is not statistically significant at the 5% level (P >0.05). In other words, we cannot exclude chance as an explanation for treatment differences of this magnitude with a sample of this size.
Table 7-1. Results of a hypothetical trial concerning the 12-month outcome of success or failure in patients with the targeted disease.
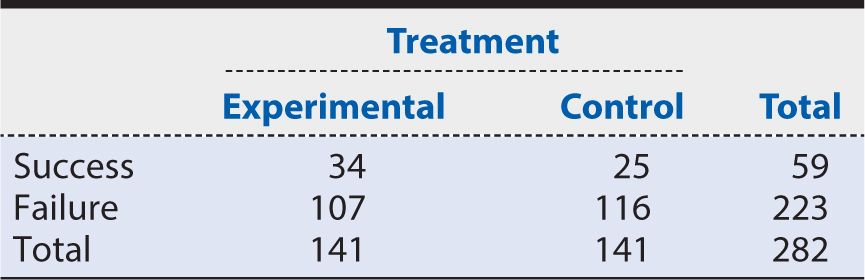
Alternative approaches of reporting the treatment effect include percentage absolute risk reduction (or benefit), relative risk or number needed to treat (NNT), which is the number of patients needed to be treated with the experimental treatment rather than the control treatment for one additional patient to benefit. Using the data in Table 7-1, we can calculate these measures as follows:
Percent absolute risk reduction or Benefit
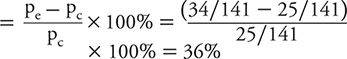
This means that the experimental group had about a one third improvement in response likelihood compared with the baseline response among controls.
![]()
This means that the likelihood of a successful response was 36% higher within the experimental group when compared with the control group.
![]()
Where ARR is the Absolute Risk Reduction. This means that almost 16 patients need to be treated with the experimental method in order to have one more patient respond than would otherwise.
All of these summary measures are acceptable for reporting clinical trial data. For this particular example, the measures should be interpreted as follows: being treated with the experimental therapy provides about one third more successful outcomes than the control therapy, the risk of having a beneficial (successful) outcome in the experimental treatment group is about one third greater than in the control group, and the experimental treatment will lead to one more success for every 16 patients treated. Choosing which metric to report is a decision that should be based on what the study team believes is most important for their audience to know in order to understand the magnitude of the treatment effect. Sometimes a combination of the measures is provided. In addition to these various point estimates, the reported value should be accompanied by a two-sided CI to show the uncertainty in the estimate. Although the point estimate tells us something about the treatment effect, the point estimate alone does not provide information on whether this value is statistically different from no effect. By including the CI, we are providing valuable information on the statistical precision of our estimate. For example, the risk ratio is 1.36 in the above example and has a 95% CI of 0.86, 2.16. A risk ratio of 1 indicates that there is no difference between the two treatments (Pe = Pc) and as it moves away from 1 we begin to see greater differences in outcomes between the groups. The CI provides a range of plausible values for the risk ratio, and because the interval includes 1, we can conclude that there is no statistical difference (at P < 0.05) between the two treatment arms. A similar approach can be seen with the reported interval for the absolute risk reduction (ARR) or benefit. In that scenario, an interval that contains zero indicates no risk difference between the two treatment arms (pe = pc).
It should be noted that odds ratios (ORs) were not part of the above approaches. Although ORs are valid measures and sometimes reported in clinical trials, the data from trials are often interpreted as the proportion that “do better” on treatment compared with control. This is the interpretation of a risk ratio, not an OR. The OR, often used for case control studies (see Chapter 9), provides the relative odds that a patient would “do better” if he or she received the treatment compared with the control and is calculated as follows:
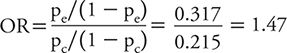
Odds ratios and risk ratios give similar values only when the proportion of events is small, but as that proportion increases, the two values can give very different results. The OR for the data in Table 7-1 is 1.47, which is slightly larger than the reported risk ratio of 1.36. Although both measures are valid, the interpretation of the results guides which relative measure to report. In trials, we commonly report the risk ratio or absolute risk reduction or benefit.
Often clinical trial analyses include a known prognostic variable, a variable that impacts outcome regardless of treatment. For example, in certain acute neurologic diseases such as stroke, traumatic brain injury, and spinal cord injury, the baseline severity of the injury impacts outcome such that more severe cases tend to have worse functional outcomes. The analysis for these outcomes often includes an adjustment for baseline severity to account for the impact of severity on outcome because our true focus is the impact of treatment on outcome regardless of severity. The treatment effect within each subgroup of severity may be of secondary interest; however, the study often lacks sufficient statistical power for subgroup analysis. Overall, if the incorrect analysis method is used, then correct inferences about treatment effect cannot be made, and the trial will lack validity. Table 7-2 provides a basic guide for analysis choices.
Table 7-2. Outcomes and common analyses.

In addition to choosing the correct analysis, it is important to analyze the correct population. In randomized clinical trials, the primary analysis should be conducted on the intent-to-treat population, which is defined by the randomization assignment. If a participant was randomized to receive the experimental treatment and it is known that he or she ended up never receiving it, that participant should still be analyzed as part of the experimental arm. Although this may seem illogical at first, the intent-to-treat population is a more unbiased representation of the population with the disease being studied. The reason it is less biased is that there are several scenarios in which a participant may not receive the assigned treatment, including clinical errors and participant choice if the experimental treatment has negative side effects or if the participant forgets to take the treatment or drops out of the study. Not receiving the experimental therapy can be similar, in some situations, to being in the control arm. We do not want to analyze the data by moving those individuals to the control arm, however, because then we lose the benefits of randomization as described earlier. In addition, these scenarios can occur outside of the trial in the general population with the disease. When we interpret results from a trial, particularly a phase III definitive trial, we want the results to be generalizable to patients outside of the trial. Accordingly, it is recommended to be conservative in the estimate of a treatment effect and report the results using the intent-to-treat population.
Another important aspect of outcomes and analysis is the handling of missing data. In clinical trials, missing outcome data is to be expected. Study participants may miss a follow-up visit, may withdraw consent, or may move and be unable to be followed for the remainder of the study. All of these scenarios can contribute to missing data, which impacts the data analysis. As mentioned earlier, in an intent-to-treat analysis, we would not remove participants with missing outcome data from the analysis. Instead, we have to keep them in the analysis population in order to reduce the potential bias of our treatment estimate. There are several methods for imputing data for missing observations, but this is beyond the scope of this chapter. The overall goal in the design and conduct of a trial is to minimize the amount of missing data by ensuring that outcomes of interest can be measured in all participants, the length of participant follow-up is reasonable, and there is frequent contact with the participants throughout the follow-up period.
One other point to consider is categorizing a continuous endpoint. Although dichotomous outcomes may in some situations provide simplified clinical interpretation, categorization comes with a price. Knowledge of the correct categories is not always available and thus could lead to incorrect results. Caution should be taken when attempting to categorize a continuous outcome. If possible, the existing literature should be reviewed, and the properties of an ideal outcome should be considered.
CONCLUSIONS AND LIMITATIONS
Although clinical trials are an invaluable source of information to drive innovation and improvements in clinical practice, there are a number of challenges facing the clinical research enterprise (Sung et al., 2003). In recent years, there have been concerns expressed over the disconnect between the promise of basic science discovery and the delivery of better health care. This is, in part, due to the failure to translate the findings from clinical trials, often conducted in highly controlled environments, into everyday clinical practice. The reasons for this failure are multifaceted and have led to a new area of research known as implementation and dissemination science (see Chapter 17). In addition, there are problems with the clinical research environment. It is burdened by rising costs, increasing regulatory controls, and a shortage of qualified investigators and research participants. It is important to engage the public more effectively in clinical research, both as research participants and advocates for research funding. In addition, wider participation of diverse populations in clinical trials will improve the generalizability and applicability of the information gained from the trials. Adaptive trials and PCTs address some of these issues, but there still is a need to develop new clinical trial methodologies and creative approaches to the use of data to examine and improve clinical practice in a timely manner. In addition, efforts to standardize and streamline regulatory processes are critical to improving the efficiency and cost-effectiveness of clinical trials. In conclusion, clinical trials have contributed tremendously to evidence-based clinical practice. Improvements in the approach to clinical trial design and analysis will help to make the information gained through clinical trials even more relevant to efforts to improve clinical practice and health outcomes.
SUMMARY
In summary, a well-designed and conducted clinical trial is essential for therapeutic development. The various clinical trial phases are a gradual progression to addressing the overall question of safety and efficacy. Phase I designs focus on finding the correct dose or treatment regimen to move forward in future studies. Phase II designs focus on further assessment of safety and identifying a signal of efficacy. Phase III designs continue to assess safety and focus on determining efficacy. Phase IV or postmarketing trials further refine safety and efficacy in large clinical populations. There are several study designs to choose from for each trial phase, and the choice should be driven by the primary study question and the goal of reducing biases in order to make correct inferences from the collected data. Features of good trial design include use of a concurrent control group, implementation of randomization and blinding when the design includes two or more treatment arms, a primary outcome that is valid and reliable, sample size estimation that is based on the primary outcome and the clinically relevant difference of interest, and a study population that represents the patient population of interest. In addition to good design, the analysis should complement the design in terms of accounting for the correct variability (e.g., independent vs. paired outcomes) and inclusion of important prognostic variables. The combination of appropriate trial design and analysis promotes unbiased inference of the treatment effect with the best possible precision.
The design and conduct of trials is a team effort composed not only of the clinician but also the statistician, study coordinator, and patients. This chapter introduces readers to key concepts of clinical trials and hopefully provokes further interest in the topic. Clinical trials are quite complex, and design methodology continues to be developed to improve the efficiency of these research studies. The best clinical trial lesson is to become involved in the design and conduct of a trial after becoming familiar with the basic terminology and concepts. Each trial introduces a new lesson on the methodology as well as the practical aspects of conducting a clinical trial.
1. What are the properties that classify research as a clinical trial?
A. A prospective experiment of an intervention with a control group that is conducted in humans
B. The retrospective analysis of data that was collected on humans exposed to a certain intervention
C. The testing of a new intervention on humans or animals
D. None of the above
2. What type of design would allow one to study an interaction effect?
A. Crossover design
B. Parallel design
C. Adaptive design
D. Factorial design
3. Why do we randomize trials?
A. To avoid selection bias
B. To ensure treatment assignment balance within a certain prognostic variable
C. To ensure valid statistical tests
D. All of the above
4. What makes an ideal primary outcome?
A. One that can be easily dichotomized
B. One that is a short-term endpoint
C. One that is valid and reliable
D. Both A and C
5. What phase of clinical trial development assesses what dose to use?
A. Phase III
B. Translational
C. Phase II
D. Phase I
6. Women are considered a vulnerable population.
A. True
B. False
7. A prognostic variable is
A. a variable that impacts the outcome regardless of treatment.
B. something to be avoided in trials.
C. a variable that impacts the outcome because of treatment.
D. none of the above.
8. Sample size estimation is based on
A. the primary outcome.
B. the subgroup of interest.
C. all of the outcomes one wants to examine.
D. both A and B.
9. The statistical power of a trial is the likelihood of detecting a difference if one truly exists.
A. True
B. False
10. The most important data point an investigator can contribute for sample size estimation is
A. type I error rate.
B. variance of the outcome measure based on the literature.
C. the clinically relevant difference.
D. the dollar amount that he or she has to spend on the trial.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree